
已知数列 的前n项和为
的前n项和为 ,且满足
,且满足 ,
,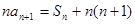 .
.
(1)求数列 的通项公式
的通项公式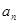 ;
;
(2)设 为数列{
为数列{ }的前n项和,求
}的前n项和,求 ;
;
(3)设 ,证明:
,证明: .
.
(1) (2)
(2)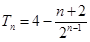 (3)见解析
(3)见解析
解析试题分析:
(1)当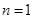 带入式子
带入式子 结合
结合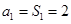 即可得到
即可得到 的值,当
的值,当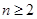 时,利用
时,利用 与
与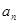 的关系(
的关系(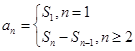 )即可得到
)即可得到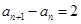 是一个常数,即可得到数列
是一个常数,即可得到数列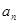 为等差数列,但是需要验证
为等差数列,但是需要验证 是否符合,进而证明
是否符合,进而证明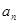 为等差数列,即可求的通项公式.
为等差数列,即可求的通项公式.
(2)把(1)中得到的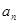 的通项公式带入
的通项公式带入 可得
可得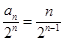 ,即为等差数列与等比数列的乘积,故需要利用错位相减法来求
,即为等差数列与等比数列的乘积,故需要利用错位相减法来求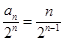 的前n项和
的前n项和 .
.
(3)把(1)得到的 带入
带入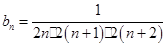 ,观察
,观察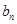 的通项公式为分式,为求其前n项和可以考虑利用裂项求和法.进行裂项
的通项公式为分式,为求其前n项和可以考虑利用裂项求和法.进行裂项 ,在进行求和就可以得到
,在进行求和就可以得到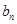 的前n项和为
的前n项和为 ,利用
,利用 非负即可证明原不等式.
非负即可证明原不等式.
试题解析:
(1)由题意,当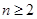 时,有
时,有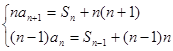 , (1分)
, (1分)
两式相减得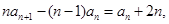 即
即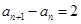 . (2分)
. (2分)
由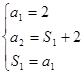 ,得
,得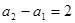 .
.
所以对一切正整数n,有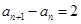 , (3分)
, (3分)
故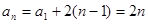 ,即
,即 . (4分)
. (4分)
(2)由(1),得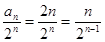 ,
,
所以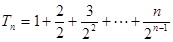 ① (5分)
① (5分)
①两边同乘以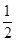 ,得
,得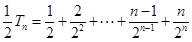 ② (6分)
② (6分)
①-②,得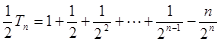 , (7分)
, (7分)
所以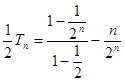 , (8分)
, (8分)
故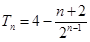 . (9分)
. (9分)
(3)由(1),得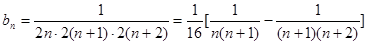 (12分)
(12分)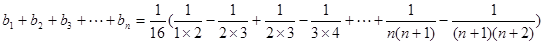
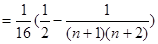 (13分)
(13分) . (14分)
. (14分)
考点:裂项求和 错位相减 不等式


科目:高中数学 来源: 题型:填空题
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给五人,使每人成等差数列,且使最大的三份之和的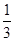 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设等比数列{an}的前n项和为Sn.已知an+1=2Sn+2( )
)
(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成一个公差为dn的等差数列,
①在数列{dn}中是否存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②求证: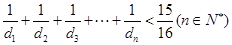 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知n∈N*,数列{dn}满足dn=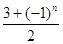 ,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,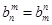 .
.
(1)求数列{an}和数列{bn}的通项公式;
(2)将数列{bn}中的第a1项,第a2项,第a3项,…,第an项删去后,剩余的项按从小到大的顺序排成新数列{cn},求数列{cn}的前2013项和T2013.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列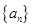 具有性质:①
具有性质:①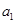 为整数;②对于任意的正整数
为整数;②对于任意的正整数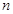 ,当
,当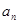 为偶数时,
为偶数时,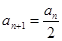 ;当
;当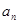 为奇数时,
为奇数时,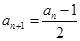 .
.
(1)若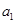 为偶数,且
为偶数,且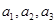 成等差数列,求
成等差数列,求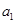 的值;
的值;
(2)设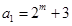 (
(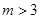 且
且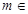 N),数列
N),数列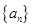 的前
的前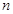 项和为
项和为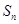 ,求证:
,求证: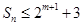 ;
;
(3)若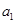 为正整数,求证:当
为正整数,求证:当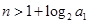 (
(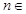 N)时,都有
N)时,都有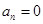 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com