
分析 利用数学归纳法证明即可.
解答 证明:①当n=1时,左边=1×22-2×32=-14,
右边=-(1+1)(4×1+3)=-14,
等时成立;
②假设当n=k(k≥1)时,有1×22-2×32+…+(2k-1)(2k)2-2k(2k+1)2=-k(k+1)(4k+3),
则当n=k+1时,1×22-2×32+…+(2k-1)(2k)2-2k(2k+1)2+(2k+1)(2k+2)2-2(k+1)(2k+3)2
=-k(k+1)(4k+3)+(2k+1)(2k+2)2-2(k+1)(2k+3)2
=-k(k+1)(4k+3)+(k+1)[4(2k+1)(k+1)-2(2k+3)2]
=-k(k+1)(4k+3)-2(k+1)(6k+7)
=-(k+1)(4k2+15k+14)
=-(k+1)(k+2)(4k+7),
即当n=k+1时,等式也成立;
由①②可知等时成立.
点评 本题考查数学归纳法,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=cosx | C. | y=-sinx | D. | y=-cosx |
查看答案和解析>>
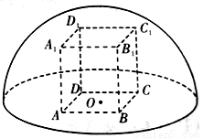
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
如图所示,直四棱柱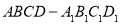 内接于半径为
内接于半径为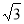 的半球
的半球 ,四边形
,四边形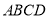 为正方形,则该四棱柱的体积最大时,
为正方形,则该四棱柱的体积最大时,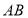 的长为( )
的长为( )
A. B.
B.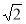 C.
C.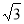 D.
D.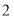
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
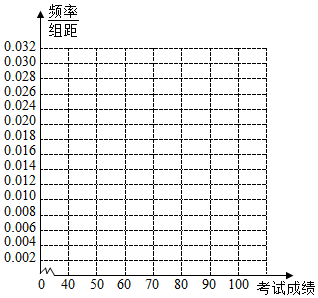
| 成绩 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 2 | 8 | 15 | 15 | 4 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com