
| A. | y=sinx | B. | y=cosx | C. | y=-sinx | D. | y=-cosx |
分析 利用正弦函数和余弦函数的图象和性质求解.
解答 解:在A中,∵sin$\frac{π}{2}$=1,∴y=sinx的图象不经过点($\frac{π}{2}$,-1),故A错误;
在B中,∵cos$\frac{π}{2}$=0,∴y=cosx的图象不经过点($\frac{π}{2}$,-1),故B错误;
在C中,∵sin$\frac{π}{2}$=1,∴y=-sinx的图象不经过点($\frac{π}{2}$,-1),故C正确;
在D中,∵cos$\frac{π}{2}$=0,∴y=cosx的图象不经过点($\frac{π}{2}$,-1),故D错误.
故选:C.
点评 本题考查图象是否过定点的判断,是基础题,解题时要认真审题,注意正弦函数与余弦函数的性质的合理运用.


科目:高中数学 来源: 题型:选择题
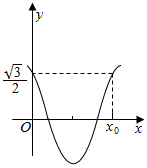 已知函数f(x)=2cos(πx)•cos2$\frac{φ}{2}$-sin(πx)•sinφ-cos(πx)(0≤φ<$\frac{π}{2}$)的部分图象如图所示,则图中的x0的值为( )
已知函数f(x)=2cos(πx)•cos2$\frac{φ}{2}$-sin(πx)•sinφ-cos(πx)(0≤φ<$\frac{π}{2}$)的部分图象如图所示,则图中的x0的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{7}{3}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
六个面都是平行四边形的四棱柱称为平行六面体.如图甲,在平行四边形ABCD中,有AC2+BD2=2(AB2+AD2),那么在图乙所示的平行六面体ABCD-A1B1C1D1中,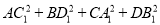 等于( )
等于( )
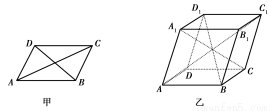
A.2(AB2+AD2+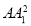 )
)
B.3(AB2+AD2+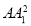 )
)
C.4(AB2+AD2+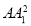 )
)
D.4(AB2+AD2)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com