
| A. | c<b<a | B. | b<a<c | C. | c<a<b | D. | a<c<b |
分析 根据条件可得到x≥0时,f(x+1)=1-2x+1,而根据f(x+1)为偶函数即可得到f(1-x)=1-2x+1,x≥0,从而可求出f($\frac{2}{3}$),$f(\frac{1}{3})$,$f(\frac{3}{2})$,并根据指数函数单调性比较这三个数的大小.
解答 解:根据题意,x≥0时,f(x+1)=1-2x+1;
∵f(x+1)为偶函数;
∴f(-x+1)=f(x+1);
∴f(1-x)=1-2x+1,x≥0;
∴$f(\frac{2}{3})=f(1-\frac{1}{3})=1-{2}^{\frac{4}{3}}$,$f(\frac{1}{3})=f(1-\frac{2}{3})=1-{2}^{\frac{5}{3}}$,$f(\frac{3}{2})=1-{2}^{\frac{3}{2}}$;
$\frac{4}{3}<\frac{3}{2}<\frac{5}{3}$,∴${2}^{\frac{4}{3}}<{2}^{\frac{3}{2}}<{2}^{\frac{5}{3}}$;
∴c<a<b.
故选C.
点评 考查已知f(x)求f(1+x)的方法,及这两函数自变量的范围的不同,偶函数的定义,以及指数函数的单调性.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:选择题
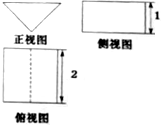 《九章算术》中,将底面是直角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的表面积为( )| A. | 4+2$\sqrt{2}$ | B. | 2 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知A,B,C,D为圆O上的四点,直线PA切圆O于点A,PA∥BD,AC与BD相交于G点.
已知A,B,C,D为圆O上的四点,直线PA切圆O于点A,PA∥BD,AC与BD相交于G点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com