
在如图的多面体中,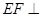 平面
平面 ,
, ,
,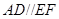 ,
,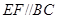 ,
,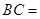
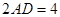 ,
,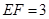 ,
,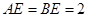 ,
,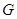 是
是 的中点.
的中点.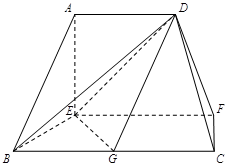
(1)求证: 平面
平面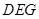 ;
;
(2)求证: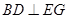 ;
;
(3)求三棱锥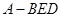 的体积.
的体积.
(1)详见解析;(2)详见解析;(3)三棱锥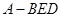 的体积为
的体积为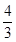 .
.
解析试题分析:(1)证明四边形 为平行四边形,进而得到
为平行四边形,进而得到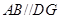 ,再利用直线与平面平行的判定定理得到
,再利用直线与平面平行的判定定理得到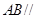 平面
平面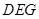 ;(2)过点
;(2)过点 作
作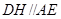 交
交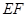 于点
于点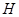 ,连接
,连接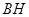 、
、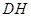 、
、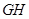 ,先证明
,先证明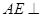 平面
平面 ,于是得到
,于是得到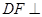 平面
平面 ,从而得到
,从而得到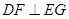 ,再证明四边形
,再证明四边形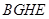 为菱形,从而得到
为菱形,从而得到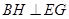 ,利用直线与平面垂直的判定定理得到
,利用直线与平面垂直的判定定理得到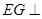 平面
平面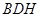 ,从而得到
,从而得到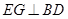 ;(3)由
;(3)由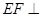 平面
平面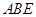 ,由
,由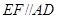 ,得到
,得到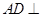 平面
平面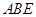 ,从而将三棱锥
,从而将三棱锥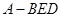 的体积的计算变换成以点
的体积的计算变换成以点 为顶点,以
为顶点,以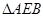 所在平面为底面的三棱锥来计算体积.
所在平面为底面的三棱锥来计算体积.
试题解析:(1)∵AD∥EF,EF∥BC,∴AD∥BC.
又∵BC=2AD,G是BC的中点,∴AD//BG,
∴四边形ADGB是平行四边形,∴AB∥DG.
∵AB?平面DEG,DG?平面DEG,∴AB∥平面DEG.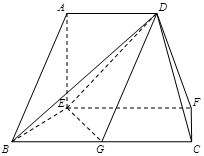
(2)证明:∵EF⊥平面AEB,AE?平面AEB,∴EF⊥AE,
又AE⊥EB,EB∩EF=E,EB,EF?平面BCFE,∴AE⊥平面BCFE.
过D作DH∥AE交EF于H,则DH⊥平面BCFE.
∵EG?平面BCFE,∴DH⊥EG.
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,
∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG,
又BH∩DH=H,BH?平面BHD,DH?平面BHD,∴EG⊥平面BHD.
∵BD?平面BHD,∴BD⊥EG.(10分)
(3)∵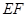 ⊥平面
⊥平面 ,EF//AD,∴AD⊥平面
,EF//AD,∴AD⊥平面 ,故三棱锥A-BED的高为AD
,故三棱锥A-BED的高为AD
∵ ,∴S△AEB =
,∴S△AEB =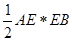 =
=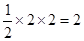
∴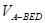 =
=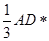 S△AEB=
S△AEB=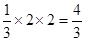 (14分)
(14分)
考点:1.直线与平面平行;2.异面直线垂直;3.等体积法计算三棱锥的体积


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC-A1B1C1中,C1C⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.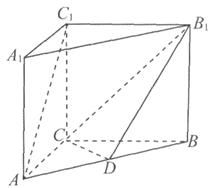
(1)求证:AC1∥平面CDB1;
(2)求三棱锥D-B1C1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD丄CD,AB//CD,AB=AD=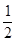 CD=2,点M在线段EC上.
CD=2,点M在线段EC上.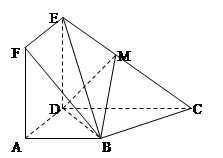
(I)当点M为EC中点时,求证: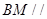 面
面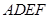 ;
;
(II)求证:平面BDE丄平面BEC;
(III)若平面说BDM与平面ABF所成二面角锐角,且该二面角的余弦值为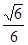 时,求三棱锥M-BDE的体积.
时,求三棱锥M-BDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =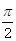 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .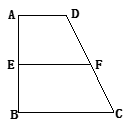
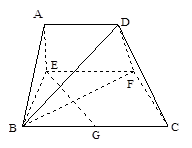
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当f(x)取得最大值时,求二面角D-BF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为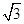 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.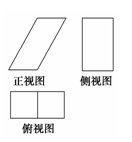
(1)求该几何体的体积V;
(2)求该几何体的表面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一个几何体的三视图如图所示。(1)求此几何体的表面积;(2)如果点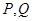 在正视图中所示位置:
在正视图中所示位置: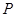 为所在线段中点,
为所在线段中点,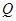 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从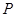 点到
点到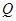 点的最短路径的长。
点的最短路径的长。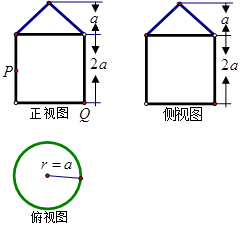
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com