
 某人在草地上散步,看到他西方有两根相距6米的标杆A、B,当他向正北方向步行3分钟后,看到标杆B在其西南方向上,根标杆A在其南偏西30°方向上,求此人步行的速度.(要求用铅笔画出图形,标出字母与相关数据)
某人在草地上散步,看到他西方有两根相距6米的标杆A、B,当他向正北方向步行3分钟后,看到标杆B在其西南方向上,根标杆A在其南偏西30°方向上,求此人步行的速度.(要求用铅笔画出图形,标出字母与相关数据) 分析 根据正弦定理和解直角三角形即可求出.
解答 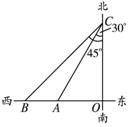 解:如图所示,
解:如图所示,
A、B两点的距离为6米,当此人沿正北方向走到C点时,测得∠BCO=45°,∠ACO=30°,
∴∠BCA=∠BCO-∠ACO=45°-30°=15°.
由题意,知∠BAC=120°,∠ABC=45°.
在△ABC中,由正弦定理,得$\frac{AC}{sin∠ABC}$=$\frac{AB}{sin∠BCA}$,即有AC=$\frac{6×sin45°}{sin15°}$=6$\sqrt{3}$+6
在Rt△AOC中,有
OC=AC•cos30°=(6$\sqrt{3}$+6)×$\frac{\sqrt{3}}{2}$=9+3$\sqrt{3}$,
设步行速度为x米/分,
则x=$\frac{9+3\sqrt{3}}{3}$=3+$\sqrt{3}$≈4.73.
即此人步行的速度约为4.73米/分.
点评 本题考查了解三角形的问题,关键是掌握正弦定理,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4034 | B. | 4032 | C. | 4030 | D. | 4028 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1007 | B. | 1006 | C. | 2014 | D. | 2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e}{2}$ | B. | 2 | C. | 1 | D. | $\frac{e}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com