
分析 (1)根据奇偶性的定义直接判断即可.
(2)分离参数法,转化成二次函数问题求解.
解答 解:(1)函数f(x)=2x+$\frac{a}{2^x}$-1(a为实数).
当a=1时,f(x)=2x+2-x-1,
∵f(-x)=2-x+2x-1=f(x),
∴y=f(x)为偶函数.
(2)由题意:函数f(x)=2x+$\frac{a}{2^x}$-1(a为实数).
任意x∈R时f(x)≥0,即2x+$\frac{a}{2x}$-1≥0
?a≥2x-(2x)2,
令t=2x>0,则:a≥-t2+t(t>0).
对任意x∈R时f(x)≥0恒成立,只要当t>0时,a≥(-t2+t)max.
根据二次函数的图象及性质:
可得:当t=$\frac{1}{2}$时,可得(-t2+t)max=$\frac{1}{4}$,
∴a≥$\frac{1}{4}$.
故得a的取值范围是[$\frac{1}{4}$,+∞).
点评 本题考查了函数的奇偶性的判断和分离参数法转化为二次函数问题解决恒成立问题.属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:填空题
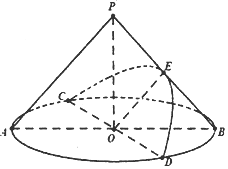 如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为$\sqrt{10}$.
如图,在底面半径和高均为4的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,若过直径CD与点E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某人在草地上散步,看到他西方有两根相距6米的标杆A、B,当他向正北方向步行3分钟后,看到标杆B在其西南方向上,根标杆A在其南偏西30°方向上,求此人步行的速度.(要求用铅笔画出图形,标出字母与相关数据)
某人在草地上散步,看到他西方有两根相距6米的标杆A、B,当他向正北方向步行3分钟后,看到标杆B在其西南方向上,根标杆A在其南偏西30°方向上,求此人步行的速度.(要求用铅笔画出图形,标出字母与相关数据)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com