Question

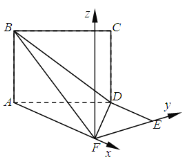
【题目】如图，平面平面，其中为矩形，为梯形，，，.

（Ⅰ）求证：平面；

（Ⅱ）若二面角的平面角的余弦值为，求的长.

Answer 1

【答案】(1)见解析；（2）AB＝.

【解析】分析：(Ⅰ)由线面垂直的性质可得平面，从而得，结合，利用线面垂直的判定定理可得平面；（Ⅱ）设，以为原点，所在的直线分别为轴，轴建立空间直角坐标系，平面ABF的法向量可取，利用向量垂直数量积为零列方程组求得平面的法向量)，利用空间向量夹角余弦公式可得结果.

详解：(Ⅰ)平面平面,且为矩形，

平面，

又平面, ，

又且

平面.源:Z+xx+k.Com]

(Ⅱ)设AB＝x．以F为原点，AF，FE所在的直线分别为x轴，y轴建立空间直角坐标系．则F(0，0，0)，A(－2，0，0)，E(0，，0)，D(－1，，0)，B(－2，0，x)，所以＝(1，－，0)，＝(2，0，－x)．

因为EF⊥平面ABF，所以平面ABF的法向量可取＝(0，1，0)．

设＝(x1，y1，z1)为平面BFD的法向量，则

所以，可取＝(，1，)．

因为cos<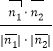，>＝＝，得x＝，所以AB＝．