
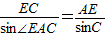 ,所以
,所以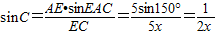 (5分)
(5分)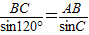 ,(7分)
,(7分)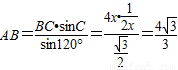 .(9分)
.(9分)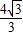 km(10分)
km(10分)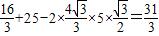 (13分)
(13分)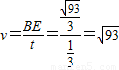 (14分)
(14分) km/h(15分)
km/h(15分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
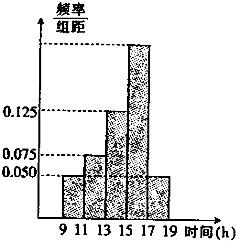 某商场在春节黄金周的促销活动中,对每天上午9时至下午19时的销售额进行统计,其频率分布直方图如图所示,已知9时至11时的销售额为2万元,则从15时至17时的销售额为
某商场在春节黄金周的促销活动中,对每天上午9时至下午19时的销售额进行统计,其频率分布直方图如图所示,已知9时至11时的销售额为2万元,则从15时至17时的销售额为查看答案和解析>>
科目:高中数学 来源: 题型:
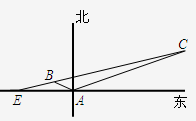
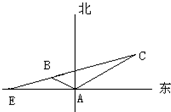 如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?查看答案和解析>>
科目:高中数学 来源: 题型:
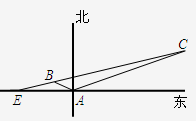 如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.
如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修5 1.2应用举例练习卷(解析版) 题型:解答题
海岛O上有一座海拔1000m的山,山顶上设有一个观察站A,上午11时测得一轮船在岛北偏东60o的C处,俯角为30o,11时10分又测得该船在岛北偏西60o的B处,俯角为60o,如图所示,求:
(1)该船的速度为每小时多少千米?
(2)若此船以匀速度继续航行,则它何时到达岛的正西方向?此时,船所在点E离开海岛多少千米?
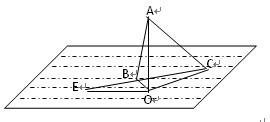
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com