
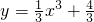 ,
,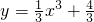 上,且y'=x2
上,且y'=x2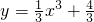 与过点P(2,4)的切线相切于点A(x0,
与过点P(2,4)的切线相切于点A(x0,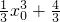 ),
),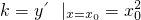 ,
,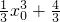 )=x02(x-x0),
)=x02(x-x0),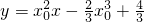
 ,即x03-3x02+4=0,
,即x03-3x02+4=0, )
) =4(x+2)
=4(x+2)

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
 (2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.
(2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
如图所示,已知曲线![]() 交于点O、A,直线
交于点O、A,直线

![]() 与曲线
与曲线![]() 、
、![]() 分别交于点D、B,连结OD,DA,AB.
分别交于点D、B,连结OD,DA,AB.
(1)求证:曲边四边形ABOD(阴影部分:OB
为抛物线弧)的面积![]() 的函数表达
的函数表达
式为 ![]()
![]()
(2)求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011年广东省佛山一中高二下学期第一次月考数学理卷 题型:解答题
(本题满分14分)
如图所示,已知曲线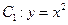 与曲线
与曲线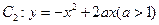 交于点O、A,直线
交于点O、A,直线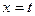 (0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。
(0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。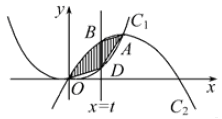
(1)写出曲边四边形ABOD(阴影部分)的面积S与t的函数关系式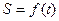 ;
;
(2)求函数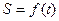 在区间
在区间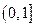 上的最大值。
上的最大值。
查看答案和解析>>
科目:高中数学 来源:2010年福建省高二第二学期半期考试数学(理科)试题 题型:解答题
(本小题满分14分)
如图所示,已知曲线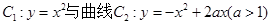 交于点O、A,直线
交于点O、A,直线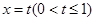 与曲线
与曲线 、
、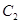 分别交于点D、B,连结OD,DA,AB.
分别交于点D、B,连结OD,DA,AB.
(1)求证:曲边四边形ABOD(阴影部分:OB为抛物线弧)的面积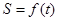 的函数表达式为
的函数表达式为 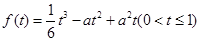

(2)求函数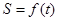 在区间
在区间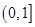 上的最大值.
上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com