
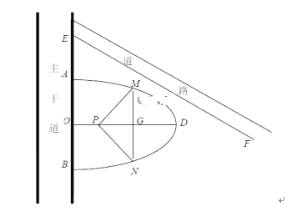
【题目】某学校决定在主干道旁边挖一个半椭圆形状的小湖,如图所示,AB=4,O为AB的中点,椭圆的焦点P在对称轴OD上,M、N在椭圆上,MN平行AB交OD与G,且G在P的右侧,△MNP为灯光区,用于美化环境.
(1)若学校的另一条道路EF满足OE=3,tan∠OEF=2,为确保道路安全,要求椭圆上任意一点到道路EF的距离都不小于![]() ,求半椭圆形的小湖的最大面积:(椭圆
,求半椭圆形的小湖的最大面积:(椭圆![]() (
(![]() )的面积为
)的面积为![]() )
)
(2)若椭圆的离心率为![]() ,要求灯光区的周长不小于
,要求灯光区的周长不小于![]() ,求PG的取值范围.
,求PG的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 的长求得
的长求得![]() 的值.首先求出直线
的值.首先求出直线![]() 所在的直线方程,设出与此直线平行,且与半椭圆相切的直线方程,利用两平行线间的距离求得相切直线的方程,代入椭圆方程利用判别式等于零求得
所在的直线方程,设出与此直线平行,且与半椭圆相切的直线方程,利用两平行线间的距离求得相切直线的方程,代入椭圆方程利用判别式等于零求得![]() 的值.(2)根据椭圆的离心率和
的值.(2)根据椭圆的离心率和![]() 的值,利用
的值,利用![]() 求得
求得![]() 的值,即求得椭圆方程,求得焦点
的值,即求得椭圆方程,求得焦点![]() 的坐标.设出
的坐标.设出![]() 点的坐标,代入椭圆方程,由此写出周长的表达式,列不等式,解不等式可求得
点的坐标,代入椭圆方程,由此写出周长的表达式,列不等式,解不等式可求得![]() 点横坐标的取值范围,减去
点横坐标的取值范围,减去![]() 后得到
后得到![]() 的取值范围.
的取值范围.
(1)因为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,
,
所以![]() 所在的直线方程为
所在的直线方程为![]() 。
。
因为椭圆上任意一点到道路![]() 的距离都小于
的距离都小于![]() ,
,
所以椭圆最大面积时与一条平行于![]() 且距离为
且距离为![]() 的直线相切,
的直线相切,
设直线![]() ,
,
由两条直线之间的距离为![]() ,所以
,所以![]() ,
,
解得![]() 或
或![]() (舍弃)
(舍弃)
设椭圆方程为![]() ,
,
由于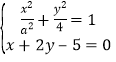 得到
得到![]()
因为直线与椭圆相切,所以![]() ,解得
,解得![]() ,
,
所以椭圆方程为![]() ,
,
所以椭圆分面积为![]() 。
。
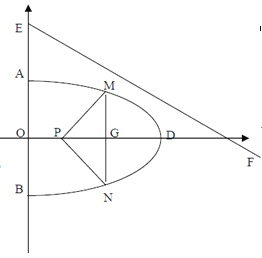
(2)设椭圆方程为![]() ,
,
因为椭圆的离心率为![]() ,所以
,所以![]() ,所以
,所以![]() 。
。
所以椭圆方程为![]()
设![]() ,则灯光区的周长
,则灯光区的周长![]()
由题意![]() ,
,
所以![]() ,所以
,所以![]()
∴ ![]() ,
,
所以![]() ,即
,即![]() ,
,
又因为![]() 在
在![]() 的右侧,所以
的右侧,所以![]() ,所以
,所以![]()
所以![]() 的取值范围是
的取值范围是![]() 。
。


科目:高中数学 来源: 题型:
【题目】若函数f(x)对定义域内的任意x1 , x2 , 当f(x1)=f(x2)时,总有x1=x2 , 则称函数f(x)为单纯函数,例如函数f(x)=x是单纯函数,但函数f(x)=x2不是单纯函数.若函数 ![]() 为单纯函数,则实数m的取值范围是 .
为单纯函数,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,|AM|=|AN|时,求△AMN的面积;
(Ⅱ)当2|AM|=|AN|时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() +ln(
+ln( ![]() +x)+
+x)+ ![]() cos xdx在区间[﹣k,k](k>0)上的值域为[m,n],则m+n的值是( )
cos xdx在区间[﹣k,k](k>0)上的值域为[m,n],则m+n的值是( )
A.0
B.2
C.4
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5. 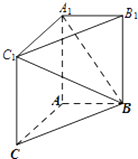
(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求证二面角A1﹣BC1﹣B1的余弦值;
(Ⅲ)证明:在线段BC1上存在点D,使得AD⊥A1B,并求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为( )
A.(﹣2,+∞)
B.(0,+∞)
C.(1,+∞)
D.(4,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com