
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
由K2= ![]() 算得,K2=
算得,K2= ![]() ≈9.616参照附表,得到的正确结论是( )
≈9.616参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C.有99%以上的把握认为“生育意愿与城市级别有关”
D.有99%以上的把握认为“生育意愿与城市级别无关”
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个 ![]() 列联表;
列联表;
(2)判断性别与休闲方式是否有关系.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为 ![]() 件时,销售所得的收入为
件时,销售所得的收入为 ![]() 万元.
万元.
(1)该公司这种产品的年生产量为 ![]() 件,生产并销售这种产品所得到的利润关于当年产量
件,生产并销售这种产品所得到的利润关于当年产量 ![]() 的函数为
的函数为 ![]() ,求
,求 ![]() ;
;
(2)当该公司的年产量为多少件时,当年所获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线 ![]() (a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+
(a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+ ![]() ,则该双曲线的离心率取值范围是( )
,则该双曲线的离心率取值范围是( )
A.(1﹣ ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2 ![]() )
)
D.(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(b8)xaab,当x(,3)∪(2,+)时,f(x)<0.
(1)求f(x)的解析式;
(2)若不等式f(x)<m的解集为R,求m的取值范围;
(3) 求不等式f(x)<m+18的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:
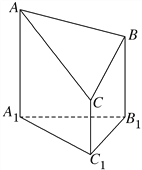
(Ⅰ)该几何体的体积;
(Ⅱ)截面ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com