[题目]已知函数f(x)=ax2+(b8)xaab.当x(.3)∪(2.+)时.f(x)<0．(1)求f(x)的解析式,(2)若不等式f(x)<m的解集为R.求m的取值范围,(3) 求不等式f(x)<m+18的解集．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数f(x)=ax2+(b8)xaab，当x(，3)∪(2，+)时，f(x)<0．

(1)求f(x)的解析式；

(2)若不等式f(x)<m的解集为R，求m的取值范围；

(3) 求不等式f(x)<m+18的解集．

【答案】（1） (2)m> (3)m>时解集为R ,m=时解集为；，m<时，解集为.

【解析】分析：（1）利用三个“二次”关系，转化为根与系数的问题；

（2）不等式f(x)<m的解集为R，即3x2+3x-18+m恒成立，故；

（3）对m分类讨论，解一元二次不等式即可.

详解：（1）由已知得，方程ax2+（b﹣8）x﹣a﹣ab=0的两个根为﹣3，2，

则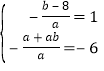，即，

解得a=﹣3，b=5，

∴f（x）=﹣3x2﹣3x+18；

(2) 不等式f(x)<m的解集为R，即﹣3x2﹣3x+18<m在R恒成立，

即3x2+3x-18+m恒成立，

∴

∴m>,

(3) 3x2+3x+m

m>时解集为R ,m=时解集为；

m<时，解集为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】函数若函数在上有3个零点，则的取值范围为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一个正四面体的“骰子”（四个面分别标有1，2，3，4四个数字），掷一次“骰子”三个侧面的数字的和为“点数”，连续抛掷“骰子”两次．
（1）设A为事件“两次掷‘骰子’的点数和为16”，求事件A发生的概率；
（2）设X为两次掷“骰子”的点数之差的绝对值，求随机变量X的分布列和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】随着国家二孩政策的全面放开，为了调查一线城市和非一线城市的二孩生育意愿，某机构用简单随机抽样方法从不同地区调查了100位育龄妇女，结果如表．

	非一线	一线	总计
愿生	45	20	65
不愿生	13	22	35
总计	58	42	100

附表：

P（K2≥k）	0.050	0.010	0.001
k	3.841	6.635	10.828

由K2= 算得，K2= ≈9.616参照附表，得到的正确结论是（）
A.在犯错误的概率不超过0.1%的前提下，认为“生育意愿与城市级别有关”
B.在犯错误的概率不超过0.1%的前提下，认为“生育意愿与城市级别无关”
C.有99%以上的把握认为“生育意愿与城市级别有关”
D.有99%以上的把握认为“生育意愿与城市级别无关”

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若函数f（x）=[x3+3x2+（a+6）x+6﹣a]e﹣x在区间（2，4）上存在极大值点，则实数a的取值范围是（）
A.（﹣∞，﹣32）
B.（﹣∞，﹣27）
C.（﹣32，﹣27）
D.（﹣32，﹣27]

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】本着健康、低碳的生活理念，租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租时间不超过两小时免费，超过两个小时的部分每小时收费2元（不足1小时的部分按1小时计算）.有甲、乙两人独立来该租车点骑游（各组一车一次）.设甲、乙不超过两小时还车的概率分别为，；两小时以上且不超过三小时还车的概率分别为，；两人租车时间都不会超过四小时.
（1）求甲、乙两人所付租车费用相同的概率；
（2）设甲、乙两人所付的租车费用之和为随机变量，求的分布列.