
����Ŀ�����Ž�������̼��������������г����ε���Խ��Խ��.ij���г������շѱ���ÿ��ÿ����ʱ�䲻������Сʱ��ѣ���������Сʱ�IJ���ÿСʱ�շ�2Ԫ������1Сʱ�IJ��ְ�1Сʱ���㣩.�мס������˶�������������Σ�����һ��һ�Σ�.��ס��Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ ![]() ��
�� ![]() ����Сʱ�����Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ
����Сʱ�����Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ ![]() ��
�� ![]() �������ʱ�䶼���ᳬ����Сʱ.
�������ʱ�䶼���ᳬ����Сʱ.
��1����ס������������������ͬ�ĸ��ʣ�
��2����ס������������������֮��Ϊ������� ![]() ����
���� ![]() �ķֲ���.
�ķֲ���.
���𰸡�
��1���⣺������ã��ף�������Сʱ�����Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ ![]() ��
�� ![]() ��
��
�Ǽס��������������������ͬΪ�¼� ![]() ����
���� ![]() ��
��
���ԣ��ס��������������������ͬ�ĸ���Ϊ ![]() ��
��
��2���⣺��ס������������ķ���֮��Ϊ ![]() ��
�� ![]() ����ȡ��ֵΪ0��2��4��6��8
����ȡ��ֵΪ0��2��4��6��8
![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
��
�ֲ���
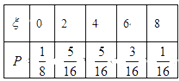
����������1������������¼�ͬʱ����������˵����ʿɷֱ���������������������ͬ�ĸ��ʼ��������ɵõ��������2���г����е� �� ����ȡ��ֵ��������֪�ֱ��������ֵ�ĸ����б����ɡ�


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����aΪʵ��������f��x��=x3��x2��x+a �� ������f��x������A��1��0��������������[��1��3]�ϵ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⣬ ![]() ������
������ ![]() �IJ���ʽ
�IJ���ʽ ![]() ��
�� ![]() ����
���� ![]() ���Ľ⼯��
���Ľ⼯�� ![]() ��
�� ![]() ������
������ ![]() �Ķ�����Ϊ
�Ķ�����Ϊ ![]() .���
.��� ![]() Ϊ�����⣬
Ϊ�����⣬ ![]() Ϊ�����⣬��ʵ��
Ϊ�����⣬��ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫���� ![]() ��a��0��b��0������ΪF1 �� ��ΪA����F1��x��Ĵ��߽�˫������P��Q���㣬��P��PM��ֱQA��M����Q��QN��ֱPA��N����PM��QN�Ľ���ΪB����B��ֱ��PQ�ľ������a+
��a��0��b��0������ΪF1 �� ��ΪA����F1��x��Ĵ��߽�˫������P��Q���㣬��P��PM��ֱQA��M����Q��QN��ֱPA��N����PM��QN�Ľ���ΪB����B��ֱ��PQ�ľ������a+ ![]() �����˫���ߵ�������ȡֵ��Χ�ǣ� ��
�����˫���ߵ�������ȡֵ��Χ�ǣ� ��
A.��1�� ![]() ��
��
B.�� ![]() ��+�ޣ�
��+�ޣ�
C.��1��2 ![]() ��
��
D.��2 ![]() ��+�ޣ�
��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)=ax2+(b8)xaab����x(��3)��(2��+)ʱ��f(x)<0��
(1)��f(x)�Ľ���ʽ��
(2)������ʽf(x)<m�Ľ⼯ΪR����m��ȡֵ��Χ��
(3) ��ʽf(x)<m+18�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ����Ȼ�����ĵ�����
����Ȼ�����ĵ����� ![]() .
.
��1������ ![]() �ĵ����������䣻
�ĵ����������䣻
��2���� ![]() ������
Ϊ������ ![]() ���ҵ�
���ҵ� ![]() ʱ��
ʱ�� ![]() �����������
����������� ![]() Ϊ
Ϊ ![]() �ĵ���������
�ĵ��������� ![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����A1B1C1Ϊ�����ֱ��������һƽ�����صõ��ļ����壬����ΪABC����֪A1B1��B1C1��2����A1B1C1��90�㣬AA1��4��BB1��3��CC1��2����
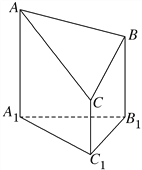
(��)�ü�����������
(��)����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ��4��4������ϵ��������̣�
��֪����C1�IJ�������Ϊ ![]() ��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ������C2�ļ����귽��Ϊ��=2sin�ȣ�
��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ������C2�ļ����귽��Ϊ��=2sin�ȣ�
��1����C1�IJ������̻�Ϊ�����귽�̣�
��2����C1��C2����ļ����꣨�ѡ�0��0�ܦȣ�2�У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
�� ![]() ������
������ ![]() ��ʹ��
��ʹ�� ![]() .����
.���� ![]() ��
�� ![]() Ϊ�桱����
Ϊ�桱���� ![]() ��
�� ![]() Ϊ�١�����ʵ��
Ϊ�١�����ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com