
【题目】已知复数z1= ![]() +(a2﹣3)i,z2=2+(3a+1)i(a∈R,i是虚数单位).
+(a2﹣3)i,z2=2+(3a+1)i(a∈R,i是虚数单位).
(1)若复数z1﹣z2在复平面上对应点落在第一象限,求实数a的取值范围;
(2)若虚数z1是实系数一元二次方程x2﹣6x+m=0的根,求实数m值.
【答案】
(1)解:由条件得,z1﹣z2=( ![]() -2)+(a2﹣3a﹣4)i
-2)+(a2﹣3a﹣4)i
因为z1﹣z2在复平面上对应点落在第一象限,故有 
∴ 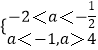 解得﹣2<a<﹣1
解得﹣2<a<﹣1
(2)解:因为虚数z1是实系数一元二次方程x2﹣6x+m=0的根
所以z1+ ![]() =
= ![]() =6,即a=﹣1,
=6,即a=﹣1,
把a=﹣1代入,则z1=3﹣2i, ![]() =3+2i,)
=3+2i,)
所以m=z1 ![]() =13
=13
【解析】(1)由题设条件,可先通过复数的运算求出的代数形式的表示,再由其几何意义得出实部与虚部的符号,转化出实数a所满足的不等式,解出其取值范围;(2)实系数一元二次方程x2﹣6x+m=0的两个根互为共轭复数,利用根与系数的关系求出a的值,从而求出m的值.
【考点精析】本题主要考查了复数的定义的相关知识点,需要掌握形如![]() 的数叫做复数,
的数叫做复数,![]() 和
和![]() 分别叫它的实部和虚部才能正确解答此题.
分别叫它的实部和虚部才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】
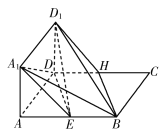
如图所示,正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() .
.
(1)若点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确的命题是( )
①P∈a,P∈αaα
②a∩b=P,bβaβ
③a∥b,aα,P∈b,P∈αbα
④α∩β=b,P∈α,P∈βP∈b.
A.①②
B.②③
C.①④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数f(x)满足:
①对任意x,y∈R,都有:f(x+y)=f(x)+f(y)﹣1;
②当x<0时,f(x)>1.
(Ⅰ)试判断函数f(x)﹣1的奇偶性;
(Ⅱ)试判断函数f(x)的单调性;
(Ⅲ)若不等式f(a2﹣2a﹣7)+ ![]() >0的解集为{a|﹣2<a<4},求f(5)的值.
>0的解集为{a|﹣2<a<4},求f(5)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)= ![]() (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[ ![]() ,2]上单调递减,那么mn的最大值为( )
,2]上单调递减,那么mn的最大值为( )
A.16
B.18
C.25
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知(a4﹣1)3+2016(a4﹣1)=1,(a2013﹣1)3+2016(a2013﹣1)=﹣1,则下列结论正确的是( )
A.S2016=﹣2016,a2013>a4
B.S2016=2016,a2013>a4
C.S2016=﹣2016,a2013<a4
D.S2016=2016,a2013<a4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC=![]()
![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD.
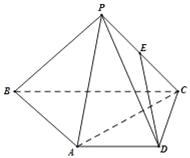
(1)证明:ED∥面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com