
°Њћвƒњ°њƒ≥≤Ќћь„∞–ё£ђ–и“™іуњйљЇЇѕ∞е![]() ’≈£ђ–°њйљЇЇѕ∞е
’≈£ђ–°њйљЇЇѕ∞е![]() ’≈£ђ“—÷™ –≥°≥ц џ
’≈£ђ“—÷™ –≥°≥ц џ![]() Ѕљ÷÷≤їЌђєжЄсµƒљЇЇѕ∞е°£Њ≠єэ≤вЋг£ђ
Ѕљ÷÷≤їЌђєжЄсµƒљЇЇѕ∞е°£Њ≠єэ≤вЋг£ђ ![]() ÷÷єжЄсµƒљЇЇѕ∞ењ…Ќђ ±љЎµ√іуњйљЇЇѕ∞е
÷÷єжЄсµƒљЇЇѕ∞ењ…Ќђ ±љЎµ√іуњйљЇЇѕ∞е![]() ’≈£ђ–°њйљЇЇѕ∞е
’≈£ђ–°њйљЇЇѕ∞е![]() ’≈£ђ
’≈£ђ ![]() ÷÷єжЄсµƒљЇЇѕ∞ењ…Ќђ ±љЎµ√іуњйљЇЇѕ∞е
÷÷єжЄсµƒљЇЇѕ∞ењ…Ќђ ±љЎµ√іуњйљЇЇѕ∞е![]() ’≈£ђ–°њйљЇЇѕ∞е
’≈£ђ–°њйљЇЇѕ∞е![]() ’≈.“—÷™
’≈.“—÷™![]() ÷÷єжЄсљЇЇѕ∞е√њ’≈
÷÷єжЄсљЇЇѕ∞е√њ’≈![]() ‘™£ђ
‘™£ђ ![]() ÷÷єжЄсљЇЇѕ∞е√њ’≈
÷÷єжЄсљЇЇѕ∞е√њ’≈![]() ‘™.Ј÷±р”√
‘™.Ј÷±р”√![]() ±н ЊєЇ¬т
±н ЊєЇ¬т![]() Ѕљ÷÷≤їЌђєжЄсµƒљЇЇѕ∞еµƒ’≈ э.
Ѕљ÷÷≤їЌђєжЄсµƒљЇЇѕ∞еµƒ’≈ э.
£®1£©”√![]() Ѕ–≥ц¬ъ„гћхЉюµƒ э—ІєЎѕµ љ£ђ≤Ґї≠≥цѕа”¶µƒ∆љ√ж«ш”т£ї
Ѕ–≥ц¬ъ„гћхЉюµƒ э—ІєЎѕµ љ£ђ≤Ґї≠≥цѕа”¶µƒ∆љ√ж«ш”т£ї
£®2£©ЄщЊЁ ©є§–и«у£ђ ![]() Ѕљ÷÷≤їЌђєжЄсµƒљЇЇѕ∞еЄч¬тґа…ў’≈ї®Ј—„ љр„о…ў£њ≤Ґ«у≥ц„о…ў„ љр э.
Ѕљ÷÷≤їЌђєжЄсµƒљЇЇѕ∞еЄч¬тґа…ў’≈ї®Ј—„ љр„о…ў£њ≤Ґ«у≥ц„о…ў„ љр э.
°Њір∞Є°њ£®1£© £ї£®2£©
£ї£®2£©![]() ÷÷љЇЇѕ∞е5’≈£ђ
÷÷љЇЇѕ∞е5’≈£ђ ![]() ÷÷љЇЇѕ∞е10’≈ї®Ј—„ љр„о…ў£ђ„о…ў„ љр эќ™1720‘™.
÷÷љЇЇѕ∞е10’≈ї®Ј—„ љр„о…ў£ђ„о…ў„ љр эќ™1720‘™.
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©ѕ»…и¬т![]() љЇЇѕ∞е
љЇЇѕ∞е![]() ’≈£ђ
’≈£ђ ![]() љЇЇѕ∞е
љЇЇѕ∞е![]() ’≈£ђЄґ≥ц„ љр
’≈£ђЄґ≥ц„ љр![]() ‘™£ђЄщЊЁіуњйљЇЇѕ∞е–и“™20’≈£ђ–°њйљЇЇѕ∞е–и“™50’≈£ђ≥йѕу≥ц
‘™£ђЄщЊЁіуњйљЇЇѕ∞е–и“™20’≈£ђ–°њйљЇЇѕ∞е–и“™50’≈£ђ≥йѕу≥ц![]() ¬ъ„гµƒћхЉю£ђљ®ЅҐ‘Љ шћхЉю£ђЉіњ…„ч≥цњ…––”т£ї£®2£©ЄщЊЁƒњ±кЇѓ э
¬ъ„гµƒћхЉю£ђљ®ЅҐ‘Љ шћхЉю£ђЉіњ…„ч≥цњ…––”т£ї£®2£©ЄщЊЁƒњ±кЇѓ э![]() £ђјы”√љЎЊаƒ£–Ќ£ђ∆љ“∆÷±ѕя’“µљ„о”≈љв£ђі”ґшњ…µ√≥ц„о…ў„ љр э.
£ђјы”√љЎЊаƒ£–Ќ£ђ∆љ“∆÷±ѕя’“µљ„о”≈љв£ђі”ґшњ…µ√≥ц„о…ў„ љр э.
‘ћвљвќц£Ї£®1£©¬т![]() љЇЇѕ∞е
љЇЇѕ∞е![]() ’≈£ђ
’≈£ђ ![]() љЇЇѕ∞е
љЇЇѕ∞е![]() ’≈£ђ”…ћв“вµ√µљ
’≈£ђ”…ћв“вµ√µљ £ђ∆љ√ж«ш”т»зЌЉ£Ї
£ђ∆љ√ж«ш”т»зЌЉ£Ї

£®2£©”……иї®Ј—„ љр![]() £ђ”…£®1£©
£ђ”…£®1£©![]() µ√
µ√![]() £ђ”…ЌЉњ…÷™µ±
£ђ”…ЌЉњ…÷™µ±![]() ±£ђ
±£ђ ![]() £®‘™£©£ђір£Ї
£®‘™£©£ђір£Ї ![]() –ЌƒЊ∞е
–ЌƒЊ∞е![]() ’≈£ђ
’≈£ђ ![]() –ЌƒЊ∞е
–ЌƒЊ∞е![]() ’≈£ђЄґ≥ц„ љр„о…ўќ™
’≈£ђЄґ≥ц„ љр„о…ўќ™![]() ‘™.
‘™.


 ”≈…ъј÷‘∞ѕµЅ–ір∞Є
”≈…ъј÷‘∞ѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ эf£®x£© «ґюіќЇѓ э£ђ«“¬ъ„гf£®0£©=1£ђf£®x+1£©©Бf£®x£©=2x+5£їЇѓ эg£®x£©=ax£®a£Њ0«“a°ў1£©
£®1£©«уf£®x£©µƒљвќц љ£ї
£®2£©»фg£®2£©= ![]() £ђ«“g[f£®x£©]°Ёkґ‘x° [©Б1£ђ1]Їг≥…ЅҐ£ђ«у µ эkµƒ»°÷µЈґќІ£Ѓ
£ђ«“g[f£®x£©]°Ёkґ‘x° [©Б1£ђ1]Їг≥…ЅҐ£ђ«у µ эkµƒ»°÷µЈґќІ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ…иЇѓ эf£®x£©=a©Б ![]() £ђ
£ђ
£®1£©»фx° [ ![]() £ђ+°ё£©£ђҐў≈–ґѕЇѓ эg£®x£©=f£®x£©©Б2xµƒµ•µч–‘≤ҐЉ”“‘÷§√ч£їҐЏ»зєыf£®x£©°№2xЇг≥…ЅҐ£ђ«уaµƒ»°÷µЈґќІ£ї
£ђ+°ё£©£ђҐў≈–ґѕЇѓ эg£®x£©=f£®x£©©Б2xµƒµ•µч–‘≤ҐЉ”“‘÷§√ч£їҐЏ»зєыf£®x£©°№2xЇг≥…ЅҐ£ђ«уaµƒ»°÷µЈґќІ£ї
£®2£©»ф„№іж‘Џm£ђn єµ√µ±x° [m£ђn] ±£ђ«°”–f£®x£©° [2m£ђ2n]£ђ«уaµƒ»°÷µЈґќІ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њѕ¬Ѕ–Їѓ э÷–£ђЉ» «≈ЉЇѓ э”÷‘Џ«шЉд£®0£ђ+°ё£©…ѕµ•µчµЁ‘цµƒ «£® £©
A.![]()
B.y=e©Бx
C.y=lg|x|
D.y=©Бx2+1
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»фAi£®i=1£ђ2£ђ3£ђ°≠£ђn£© «°чAOBЋщ‘Џ∆љ√жƒЏµƒµг£ђ«“ ![]()
![]() =
= ![]()
![]() £ђЄш≥цѕ¬Ѕ–ЋµЈ®£Ї
£ђЄш≥цѕ¬Ѕ–ЋµЈ®£Ї
°§£®1£©| ![]() |=|
|=| ![]() |=|
|=| ![]() |=°≠=|
|=°≠=| ![]() |
|
°§£®2£©| ![]() |µƒ„о–°÷µ“їґ® «|
|µƒ„о–°÷µ“їґ® «| ![]() |
|
°§£®3£©µгAЇЌµгAi“їґ®є≤ѕя
°§£®4£©ѕтЅњ ![]() Љ∞
Љ∞ ![]() ‘ЏѕтЅњ
‘ЏѕтЅњ ![]() Јљѕт…ѕµƒЌґ”∞±Ўґ®ѕаµ»
Јљѕт…ѕµƒЌґ”∞±Ўґ®ѕаµ»
∆д÷–’э»ЈµƒЄц э «£® £©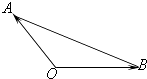
A.1Єц
B.2Єц
C.3Єц
D.4Єц
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ‘Џ°чABC÷–£ђљ«A£ђB£ђCЋщґ‘µƒ±яЈ÷±рќ™a£ђb£ђc«“b=c£ђ°ѕAµƒ∆љЈ÷ѕяќ™AD£ђ»ф ![]() =m
=m ![]()
![]() £Ѓ
£Ѓ
£®1£©µ±m=2 ±£ђ«уcosA
£®2£©µ± ![]() ° £®1£ђ
° £®1£ђ ![]() £© ±£ђ«у µ эmµƒ»°÷µЈґќІ£Ѓ
£© ±£ђ«у µ эmµƒ»°÷µЈґќІ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Їѓ э![]() ”–»эЄц≤їЌђµƒЅгµг
”–»эЄц≤їЌђµƒЅгµг![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £®∆д÷–
£®∆д÷–![]() £©£ђ‘т
£©£ђ‘т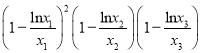 µƒ÷µќ™£® £©
µƒ÷µќ™£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њґ‘”ЏЅљЄцґ®“е”тѕаЌђµƒЇѓ эf£®x£©£ђg£®x£©£ђ»фіж‘Џ µ эm°Ґn єh£®x£©=mf£®x£©+ng£®x£©£ђ‘т≥∆Їѓ эh£®x£© «”…°∞їщЇѓ эf£®x£©£ђg£®x£©°±…ъ≥…µƒ£Ѓ
£®1£©»фf£®x£©=x2+3xЇЌЄцg£®x£©=3x+4…ъ≥…“їЄц≈ЉЇѓ эh£®x£©£ђ«уh£®2£©µƒ÷µ£ї
£®2£©»фh£®x£©=2x2+3x©Б1”…Їѓ эf£®x£©=x2+ax£ђg£®x£©=x+b£®a°Ґb° R«“ab°ў0£©…ъ≥…£ђ«уa+2bµƒ»°÷µЈґќІ£ї
£®3£©јы”√°∞їщЇѓ эf£®x£©=log4£®4x+1£©£ђg£®x£©=x©Б1°±…ъ≥…“їЄцЇѓ эh£®x£©£ђ є÷Ѓ¬ъ„гѕ¬Ѕ–Љю£ЇҐў «≈ЉЇѓ э£їҐЏ”–„о–°÷µ1£ї«уЇѓ эh£®x£©µƒљвќц љ≤Ґљш“ї≤љ—–ЊњЄ√Їѓ эµƒµ•µч–‘£®ќё–и÷§√ч£©£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ“—÷™Ћƒјв„ґ![]() ÷–£ђµ„√ж
÷–£ђµ„√ж![]() ќ™Ѕв–ќ£ђ«“
ќ™Ѕв–ќ£ђ«“![]() £ђ
£ђ ![]() «±я≥§ќ™
«±я≥§ќ™![]() µƒ’э»эљ«–ќ£ђ«“∆љ√ж
µƒ’э»эљ«–ќ£ђ«“∆љ√ж![]() ∆љ√ж
∆љ√ж![]() £ђµг
£ђµг![]() «
«![]() µƒ÷–µг.
µƒ÷–µг.
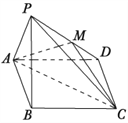
£®1£©÷§√ч£Ї ![]() ∆љ√ж
∆љ√ж![]() £ї
£ї
£®2£©«у»эјв„ґ![]() µƒћеїэ.
µƒћеїэ.
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com