
 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
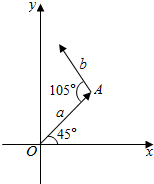 在直角坐标系中,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$如图所示,求它们的坐标.
在直角坐标系中,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$如图所示,求它们的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
已知函数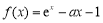 (
(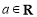 ).
).
(1)求函数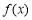 的单调区间;
的单调区间;
(2)函数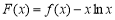 在定义域内存在零点,求
在定义域内存在零点,求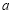 的取值范围.
的取值范围.
(3)若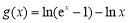 ,当
,当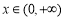 时,不等式
时,不等式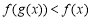 恒成立,求
恒成立,求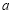 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | (5,5) | C. | (5,6) | D. | (5,7) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com