练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    [2013·郑州模拟]设α，β，γ为三个不同的平面，m，n是两条不同的直线，在命题“α∩β＝m，n?γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．
    ①α∥γ，n?β；②m∥γ，n∥β；③n∥β，m?γ.
    可以填入的条件有(　　)

    A．①或②B．②或③
    C．①或③D．①或②或③

    C

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    如图所示，ABCD－A1B1C1D1是长方体，AA1＝a，∠BAB1＝∠B1A1C1＝30°，则AB与A1C1所成的角为________，AA1与B1C所成的角为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图，在长方体各棱所在直线中，与棱所在直线互为异面直线的有     条．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    是两个不同的平面，是平面及之外的两条不同直线，给出四个论断：
    ①  ②　 ③  　④。 以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：________________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知m，n是不重合的两条直线，α，β是不重合的两个平面．下列命题：
    ①若α⊥β，m⊥α，则m∥β；      ②若m⊥α，m⊥β，则α∥β；
    ③若m∥α，m⊥n，则n⊥α；      ④若m∥α，m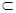β，则α∥β．
    其中所有真命题的序号是      ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知平面和直线，给出条件：
    ①；②；③；④；⑤．
    （1）当满足条件       时，有；（2）当满足条件      时，有．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图，已知正方体中，分别是的中点．则直线和所成的角为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    正三棱锥P—ABC中，∠APB=∠BPC=∠CPA=90°，PA=PB=PC=a，AB的中点M，一小蜜蜂沿锥体侧面由M爬到C点，最短路程是                            （   ）

    A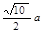．B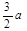．C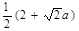．D．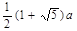

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    从正方体ABCD－A1B1C1D1的8个顶点中任意取4个不同的顶点，这4个顶点可能是：
    (1)矩形的4个顶点；
    (2)每个面都是等边三角形的四面体的4个顶点；
    (3)每个面都是直角三角形的四面体的4个顶点；
    (4)有三个面是等腰直角三角形，有一个面是等边三角形的四面体的4个顶点．
    其中正确的结论有________个．

    查看答案和解析>>

    同步练习册答案