练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    分别画出函数f(x)=(
    1
    2
    )x与g(x)=log
    1
    2
    x    的简图，并写出f（x）与g（x）的定义域、值域、单调区间．
    分析：利用指数函数和对数函数的图象，分别写出函数的定义域，值域和单调区间．
    解答：解：分别作出函数f(x)=(
    1
    2
    )x与g(x)=log
    1
    2
    x    的简图，
    则f（x）的定义域为R，值域为（0，+∞），在R上单调递减．
    g（x）的定义域为（0，+∞），值域为R，在（0，+∞）上单调递减．
    点评：本题主要考查指数函数和对数函数的图象和性质，比较基础．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　人教课标高一版(A必修1)　2009－2010学年　第11期　总167期 人教课标高一版 题型：044

    已知甲、乙两个工厂今年1月份的利润都是6万元，且甲厂2月份的利润是14万元，乙厂2月份的利润是8万元，甲、乙两个工厂的利润(万元)与月份x之间的函数关系可以分别用函数模型f(x)＝a1x2＋b1x＋6和g(x)＝a2·3x＋b2(a1，a2，b1，b2∈R)表示．

    (1)求甲、乙两个工厂今年5月份的利润；

    (2)在同一平面直角坐标系中画出函数f(x)与g(x)的大致图象，并根据图象比较今年甲、乙两个工厂的利润的大小情况．

    查看答案和解析>>

    科目：高中数学 来源：福建省南安一中2011－2012学年高一上学期期中考试数学试题 题型：044

    设函数．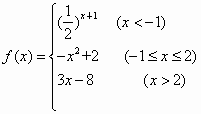

    (Ⅰ)请在下列直角坐标系中画出函数f(x)的图象；

    (Ⅱ)根据(Ⅰ)的图象，试分别写出关于x的方程f(x)＝t有2，3，4个实数解时，相应的实数t的取值范围；

    (Ⅲ)记函数g(x)的定义域为D，若存在x0∈D，使g(x0)＝x0成立，则称点(x0，x0)为函数g(x)图象上的不动点．试问，函数f(x)图象上是否存在不动点，若存在，求出不动点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省济宁市高一上学期期末模拟数学试卷（解析版） 题型：解答题

    （本小题满分12分）

    已知甲、乙两个工厂在今年的1月份的利润都是6万，且乙厂在2月份的利润是8万元．若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型：f(x)＝a1x2—4x＋6，g(x)＝a2＋b2(a1，a2，b2∈R)．

    (1)求函数f(x)与g(x)的解析式；

    (2)求甲、乙两个工厂今年5月份的利润；

    (3)在同一直角坐标系下画出函数f(x)与g(x)的草图，并根据草图比较今年1—10月份甲、乙两个工厂的利润的大小情况．

     

    查看答案和解析>>

    科目：高中数学 来源：0116 期中题 题型：解答题

    已知甲、乙两个工厂在今年的1月份的利润都是6万元，且甲厂在2月份的利润是14万元，乙厂在2月份的利润是8万元。若甲、乙两个工厂的利润（万元）与月份之间的函数关系式分别符合下列函数模型：f(x)=a1x2+b1x+6，g(x)=a2·3x+b2，(a1，a2，b1，b2∈R)。
    （1）求甲、乙两个工厂今年5月份的利润；
    （2）在同一直角坐标系下画出函数f(x)与g(x)的草图，并根据草图比较今年甲、乙两个工厂的利润的大小情况．

    查看答案和解析>>

    同步练习册答案