
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AD=DC= ![]() ,AB=PA=2
,AB=PA=2 ![]() ,且E为线段PB上的一动点.
,且E为线段PB上的一动点. 
(1)若E为线段PB的中点,求证:CE∥平面PAD;
(2)当直线CE与平面PAC所成角小于 ![]() ,求PE长度的取值范围.
,求PE长度的取值范围.
【答案】
(1)证明:取PA的中点F,连结EF,DF,

则EF∥AB,EF= ![]() AB,
AB,
又DC∥AB,DC= ![]() AB,
AB,
∴EF∥CD,EF=DC,
∴四边形EFDC是平行四边形,
∴CE∥DF,又CE平面PAD,DF平面PAD,
∴CE∥平面PAD
(2)解:∵AD=CD= ![]() ,AD⊥CD,∴AC=2,
,AD⊥CD,∴AC=2,
又AB=2 ![]() ,∠BAC=45°,∴BC=2,
,∠BAC=45°,∴BC=2,
∴AC⊥BC,
又PA⊥平面ABCD,BC平面ABCD,
∴PA⊥BC,又PA∩AC=A,
∴BC⊥平面PAC,
过E作EM∥BC,则EM⊥平面PAC,
∴∠PCE为CE与平面PAC所成的角,即∠PCE< ![]() .
.
∵PA=2 ![]() ,AC=2,∴PC=2
,AC=2,∴PC=2 ![]() ,BC=2,PB=4,
,BC=2,PB=4,
∴∠BPC= ![]() ,
,
∴当∠PCE= ![]() 时,CE⊥PB,此时PE=3,
时,CE⊥PB,此时PE=3,
∴当∠PCE ![]() 时,PE<3.
时,PE<3.
【解析】(1)取PA的中点F,连结EF,DF,证明四边形EFDC是平行四边形得出CE∥DF,故而CE∥平面PAD;(2)证明BC⊥平面PAC,可知∠PCE为CE与平面PAC所成的角,利用余弦定理得出∠BPC,利用勾股定理得出PE的最大值即可得出PE的范围.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】某兴趣小组有9名学生.若从9名学生中选取3人,则选取的3人中恰好有一个女生的概率是 ![]() .
.
(1)该小组中男女学生各多少人?
(2)9个学生站成一列队,现要求女生保持相对顺序不变(即女生 前后顺序保持不变)重新站队,问有多少种重新站队的方法?(要求用数字作答)
(3)9名学生站成一列,要求男生必须两两站在一起,有多少种站队的方法?(要求用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为正方形的四棱锥S﹣ABCD,且SD⊥平面ABCD,SD= ![]() ,AB=1,线段SB上一M点满足
,AB=1,线段SB上一M点满足 ![]() =
= ![]() ,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() : x2+y2+Dx+Ey+3=0 ,圆
: x2+y2+Dx+Ey+3=0 ,圆 ![]() 关于直线 x+y-1=0对称,圆心在第二象限,半径为
关于直线 x+y-1=0对称,圆心在第二象限,半径为![]() .
.
(1)求圆 ![]() 的方程;
的方程;
(2)已知不过原点的直线 l 与圆 ![]() 相切,且在
相切,且在 ![]() 轴、
轴、 ![]() 轴上的截距相等,求直线 l 的方程.
轴上的截距相等,求直线 l 的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x+ ![]() )的图象,只需将y=cos2x的图象上每一点( )
)的图象,只需将y=cos2x的图象上每一点( )
A.向右平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.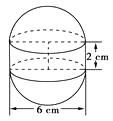
(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com