
【题目】设函数f(x)=2cos2x﹣cos(2x﹣![]() ).
).
(1)求f(x)的周期和最大值;
(2)已知△ABC中,角A.B.C的对边分别为A,B,C,若f(π﹣A)=![]() ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
【答案】(1)周期为π,最大值为2.(2)![]()
【解析】
(1)利用倍角公式降幂,展开两角差的余弦,将函数的关系式化简余弦型函数,可求出函数的周期及最值;
(2)由f(π﹣A)![]() ,求解角A,再利用余弦定理和基本不等式求a的最小值.
,求解角A,再利用余弦定理和基本不等式求a的最小值.
(1)函数f(x)=2cos2x﹣cos(2x![]() )
)
=1+cos2x![]()
=cos(2x![]() )+1,
)+1,
∵﹣1≤cos(2x![]() )≤1,
)≤1,
∴T![]() ,f(x)的最大值为2;
,f(x)的最大值为2;
(2)由题意,f(π﹣A)=f(﹣A)=cos(﹣2A![]() )+1
)+1![]() ,
,
即:cos(﹣2A![]() )
)![]() ,
,
又∵0<A<π,
∴![]() 2A
2A![]() ,
,
∴﹣2A![]() ,即A
,即A![]() .
.
在△ABC中,b+c=2,cosA![]() ,
,
由余弦定理,a2=b2+c2﹣2bccosA=(b+c)2﹣bc,
由于:bc![]() ,当b=c=1时,等号成立.
,当b=c=1时,等号成立.
∴a2≥4﹣1=3,即a![]() .
.
则a的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,其中
,其中![]() .函数
.函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为4.
与其相邻的最高点的距离为4.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)计算![]() 的值;
的值;
(Ⅲ)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间 [0,3] 上的零点个数.
在区间 [0,3] 上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2是双曲线C: ![]() (a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则C的离心率为 .
(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则C的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )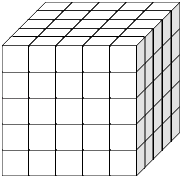
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知a1=1, ![]() ,n∈N* .
,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com