
 时,圆P恰与两直线l1、l2相切,试求圆P的方程;
时,圆P恰与两直线l1、l2相切,试求圆P的方程; 时,求四边形ABDC的面积;
时,求四边形ABDC的面积; )时,求证四边形ABDC的对角线交点位置与k的取值无关.
)时,求证四边形ABDC的对角线交点位置与k的取值无关. (AC+BD)×h,AC,BD,h用x1,y1,x2,y2,表示.代入求解.
(AC+BD)×h,AC,BD,h用x1,y1,x2,y2,表示.代入求解.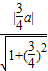 =3,解得a=5
=3,解得a=5 x 与圆P方程联立,消去x得5y2-20y+16=0,得A(
x 与圆P方程联立,消去x得5y2-20y+16=0,得A( ,
,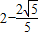 ),B(
),B(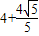 ,
, ).
). (AC+BD)×h=
(AC+BD)×h= (2y1+2y2)(x2-x1)=
(2y1+2y2)(x2-x1)= ×8×
×8×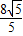 =
=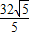 .
. )时,y=kx与圆P方程联立,并整理得:(1+k2)x2-10x+16=0,△=-64k2+36>0.x1=
)时,y=kx与圆P方程联立,并整理得:(1+k2)x2-10x+16=0,△=-64k2+36>0.x1= ,x2=
,x2=
 ,y2=
,y2=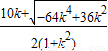 ,AC的斜率为k=
,AC的斜率为k= =
= .
. .与x 轴交与定点(
.与x 轴交与定点(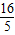 ,0)与k的值无关.
,0)与k的值无关.

科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆C:
(2013•揭阳一模)如图,设点F1(-c,0)、F2(c,0)分别是椭圆C:| x2 |
| a2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省汕头市金山中学高三(上)开学摸底数学试卷(文科)(解析版) 题型:解答题
 的左、右焦点,P为椭圆C上任意一点,且
的左、右焦点,P为椭圆C上任意一点,且 最小值为0.
最小值为0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com