
【题目】已知函数 ![]() .
.
(1)求证f(x)是R上的单调增函数;
(2)求函数f(x)的值域;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,求k的取值范围.
【答案】
(1)证明:因为 ![]() ,
,
设x1<x2∈R,则 ![]()
因为x1<x2∈R,所以 ![]() ,
, ![]() ,
,
所以f(x1)﹣f(x2)<0,故f(x)是R上的增函数
(2)解:因为 ![]() ,
,
又2x+1>1,所以 ![]() …(7分)
…(7分)
所以 ![]() ,故
,故 ![]() ,
,
所以f(x)的值域为(﹣1,1)
(3)解:因为 ![]() ,所以f(x)为奇函数,
,所以f(x)为奇函数,
所以,从而不等式f(t2﹣2t)+f(2t2﹣k)>0等价于f(t2﹣2t)>﹣f(2t2﹣k)=f(k﹣2t2)
因f(x)为增函数,由上式推得t2﹣2t>k﹣2t2,即对一切t∈R有3t2﹣2t﹣k>0
从而判别式△=4+12k<0,解得 ![]() ,
,
故实数k的取值范围是 ![]()
【解析】(1)根据增函数的定义可证明。(2)利用放缩法求出其值域。(3)利用奇函数的定义可证明f(x)为奇函数,进而转化原式等价为f(t2﹣2t)>﹣f(2t2﹣k)=f(k﹣2t2)再根据函数增减性的定义可得关于t的不等式,解得即可。
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较).


科目:高中数学 来源: 题型:
【题目】如图,平面四边形ABCD中,AB= ![]() ,AD=2
,AD=2 ![]() ,CD=
,CD= ![]() ,∠CBD=30°,∠BCD=120°.
,∠CBD=30°,∠BCD=120°.
(1)求BD的长;
(2)求∠ADC的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的方程:x2+2(a﹣1)x+2a+6=0.
(Ⅰ)若该方程有两个不等实数根,求实数a的取值范围;
(Ⅱ)若该方程有两个不等实数根,且这两个根都大于1,求实数a的取值范围;
(Ⅲ)设函数f(x)=x2+2(a﹣1)x+2a+6,x∈[﹣1,1],记此函数的最大值为M(a),最小值为N(a),求M(a),N(a)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,并且经过定点P(
,并且经过定点P( ![]() ,
, ![]() ). (Ⅰ)求椭圆E的方程;
). (Ⅰ)求椭圆E的方程;
(Ⅱ)问是否存在直线y=﹣x+m,使直线与椭圆交于A、B两点,满足OA⊥OB,若存在求m值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1、F2分别为椭圆Γ: ![]() =1(a>b>0)的左、右两个焦点,若椭圆上一点M(1,
=1(a>b>0)的左、右两个焦点,若椭圆上一点M(1, ![]() )到两个焦点的距离之和等于4.又已知点A是椭圆的右顶点,直线l交椭圆Γ于E、F两点(E、F与A点不重合),且满足AE⊥AF. (Ⅰ) 求椭圆的标准方程;
)到两个焦点的距离之和等于4.又已知点A是椭圆的右顶点,直线l交椭圆Γ于E、F两点(E、F与A点不重合),且满足AE⊥AF. (Ⅰ) 求椭圆的标准方程;
(Ⅱ) O为坐标原点,若点P满足2 ![]() ,求直线AP的斜率的取值范围.
,求直线AP的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB. 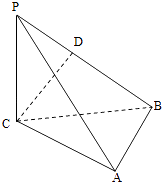
(1)求证:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com