
分析 根据函数f(x)是奇函数,将不等式f(m)+f(2m-1)>0移项,整理得f(m)>f(1-2m).因为函数是定义在(-2,2)上的减函数,所以有-2<m<1-2m<2,解之即得实数m的取值范围.
解答 解:∵f(m)+f(2m-1)>0
∴移项,得f(m)>-f(2m-1)
又∵f(x)在(-2,2)上为奇函数
∴-f(2m-1)=f(1-2m)
且-2<2m-1<2…①,
∴f(m)>f(1-2m)
又∵f(x)在[0,2)上为减函数,
∴f(x)是定义在(-2,2)上的减函数
∴m<1-2m且-2<m<2…②,
联解①②,得-$\frac{1}{2}$<m<$\frac{1}{3}$,∴实数m的取值范围为(-$\frac{1}{2}$,$\frac{1}{3}$).
点评 本题给出一个定义在(-2,2)上的抽象函数,在已知其单调性和奇偶性的情况下,解关于m的不等式,着重考查了函数奇偶性与单调性的综合应用,属于基础题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | ±1 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
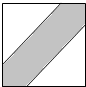 如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )| A. | $\frac{529}{625}$ | B. | $\frac{96}{625}$ | C. | $\frac{23}{25}$ | D. | $\frac{2}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com