
分析 由已知得A>B.在BC上取D,使得BD=AD,连接AD,设BD=x,则AD=x,DC=5-x.在△ADC中,cos∠DAC=cos(A-B)=$\frac{31}{32}$,由余弦定理求出x=4,从而cosC=$\frac{1}{2}$•$\frac{CD}{AC}$=$\frac{1}{8}$,再由余弦定理能求出AB.
解答 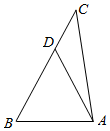 解:∵在△ABC中,a=5,b=4,cos(A-B)=$\frac{31}{32}$,
解:∵在△ABC中,a=5,b=4,cos(A-B)=$\frac{31}{32}$,
∴a>b,∴A>B.在BC上取D,使得BD=AD,连接AD,
设BD=x,则AD=x,DC=5-x.
在△ADC中,cos∠DAC=cos(A-B)=$\frac{31}{32}$,
由余弦定理得:(5-x)2=x2+42-2x•4•$\frac{31}{32}$,
即:25-10x=16-$\frac{31}{4}$x,
解得:x=4.
∴在△ADC中,AD=AC=4,CD=1,
∴cosC=$\frac{1}{2}$•$\frac{CD}{AC}$=$\frac{1}{8}$,
∴AB=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{25+16-2×5×4×\frac{1}{8}}$=6.
故答案为:$\frac{1}{8}$,6.
点评 本题考查三角形角的余弦值及边长的求法,考查余弦定理、三角形性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{4}$] | B. | (-$\frac{1}{4}$,2) | C. | [2,+∞) | D. | [0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P1>P2 | B. | P1=P2 | ||
| C. | P1<P2 | D. | P1与P2的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示(网格纸上正方形的边长为1),则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示(网格纸上正方形的边长为1),则该“堑堵”的表面积为( )| A. | 8 | B. | 16+8$\sqrt{2}$ | C. | 16+16$\sqrt{2}$ | D. | 24+16$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com