
若实数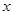 、
、 、
、 满足
满足 ,则称
,则称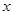 比
比 接近
接近 .
.
(1)若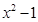 比3接近0,求
比3接近0,求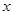 的取值范围;
的取值范围;
(2)对任意两个不相等的正数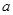 、
、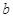 ,证明:
,证明: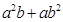 比
比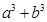 接近
接近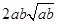 ;
;
(3)已知函数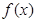 的定义域
的定义域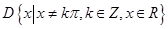 .任取
.任取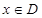 ,
,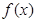 等于
等于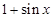 和
和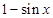 中接近0的那个值.写出函数
中接近0的那个值.写出函数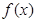 的解析式及最小值(结论不要求证明)
的解析式及最小值(结论不要求证明)
(1) xÎ(-2,2);(2) a2b+ab2比a3+b3接近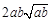 ; (3) f(x)的最小值为0。
; (3) f(x)的最小值为0。
解析试题分析:(1)根据新定义得到不等式|x2-1|<3,然后求出x的范围即可.
(2)对任意两个不相等的正数a、b,依据新定义写出不等式,利用作差法证明:a2b+ab2比a3+b3接近2ab ,
,
(3)依据新定义写出函数f(x)的解析式,f(x)= 1+sinx,x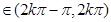
1-sinx,x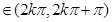
=1-|sinx|,x≠kπ直接写出它的奇偶性、最小正周期、最小值和单调性,即可.
(1) xÎ(-2,2); ---------------4分
(2) 对任意两个不相等的正数a、b,有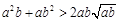 ,
,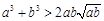 ,
,
因为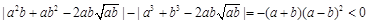 ,
,
所以 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近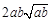 ; ------8分 (3)
; ------8分 (3) 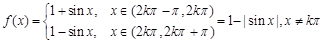 ,kÎZ,
,kÎZ,
f(x)的最小值为0, --------------------12分
考点:本题主要考查了新定义题目,直线审题是能够解题的根据,新定义问题,往往是结合相关的知识,利用已有的方法求出所求结果.注意转化思想的应用.
点评:解决该试题的关键是利用定义来表示出函数f(x)然后结合三角函数的性质来得到结论。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:单选题
若不等式|8x+9|<7和不等式ax2+bx>2的解集相等,则实数a、b的值分别为( )
| A.a=-8,b=-10 |
| B.a=-4,b=-9 |
| C.a=-1,b=9 |
| D.a=-1,b=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com