
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足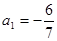 ,
,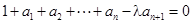 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),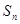 为数列{an}的前
为数列{an}的前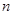 项和.
项和.
(1) 若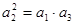 ,求
,求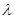 的值;
的值;
(2) 求数列{an}的通项公式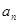 ;
;
(3) 当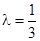 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
(1)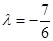 ;(2)数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列。
;(2)数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列。
【解析】
试题分析:(1) 令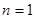 ,得到
,得到 ,令
,令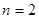 ,得到
,得到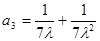 。…………2分
。…………2分
由 ,计算得
,计算得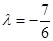 .……………………………………………………4分
.……………………………………………………4分
(2) 由题意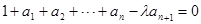 ,可得:
,可得:
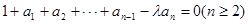 ,所以有
,所以有
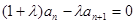
 ,又
,又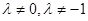 ,……………………5分
,……………………5分
得到: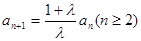 ,故数列
,故数列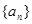 从第二项起是等比数列。……………7分
从第二项起是等比数列。……………7分
又因为 ,所以n≥2时,
,所以n≥2时,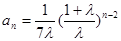 ……………………………8分
……………………………8分
所以数列{an}的通项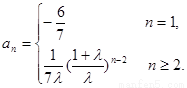 …………………………………10分
…………………………………10分
(3) 因为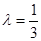 所以
所以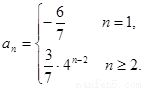 ……………………………………11分
……………………………………11分
假设数列{an}中存在三项am、ak、ap成等差数列,
①不防设m>k>p≥2,因为当n≥2时,数列{an}单调递增,所以2ak=am+ap
即:2´(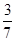 )´4k–2 =
)´4k–2 = 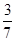 ´4m–2 +
´4m–2 + 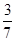 ´4p–2,化简得:2´4k - p= 4m–p+1
´4p–2,化简得:2´4k - p= 4m–p+1
即22k–2p+1=22m–2p+1,若此式成立,必有:2m–2p=0且2k–2p+1=1,
故有:m=p=k,和题设矛盾………………………………………………………………14分
②假设存在成等差数列的三项中包含a1时,
不妨设m=1,k>p≥2且ak>ap,所以2ap = a1+ak ,
2´(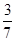 )´4p–2 = –
)´4p–2 = –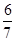 + (
+ (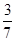 )´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1
)´4k–2,所以2´4p–2= –2+4k–2,即22p–4 = 22k–5 – 1
因为k > p ≥ 2,所以当且仅当k=3且p=2时成立………………………………………16分
因此,数列{an}中存在a1、a2、a3或a3、a2、a1成等差数列……………………………18分
考点:等差数列的性质;数列通项公式的求法;数列的递推式。
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,还考查了一定的逻辑运算与推理的能力及考查了学生通过已知条件分析问题和解决问题的能力.题目较难。


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形![]() 中,已知过点
中,已知过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() 。若
。若![]() 。
。
(1)求证:![]() 与
与![]() 的关系为
的关系为![]() ;
;
(2)设![]() ,定义函数
,定义函数![]() ,点列
,点列![]() 在函数
在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以首项为1,公比为
是以首项为1,公比为![]() 的等比数列,
的等比数列,![]() 为原点,令
为原点,令![]() ,是否存在点
,是否存在点![]()
![]() ,使得
,使得![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数![]() 为
为![]() 上偶函数,当
上偶函数,当![]() 时
时![]() ,又函数
,又函数![]() 图象关于直线
图象关于直线![]() 对称, 当方程
对称, 当方程![]() 在
在![]() 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2012届上海市崇明中学高三第一学期期中考试试题数学 题型:解答题
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
对于数列 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 称作周期为
称作周期为 的周期数列,
的周期数列, 的最小值称作数列
的最小值称作数列 的最小正周期,以下简称周期。例如当
的最小正周期,以下简称周期。例如当 时
时 是周期为
是周期为 的周期数列,当
的周期数列,当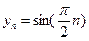 时
时 是周期为
是周期为 的周期数列。
的周期数列。
(1)设数列 满足
满足 (
( ),
), (
( 不同时为0),且数列
不同时为0),且数列 是周期为
是周期为 的周期数列,求常数
的周期数列,求常数 的值;
的值;
(2)设数列 的前
的前 项和为
项和为 ,且
,且 .
.
①若 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列 满足
满足 (
( ),
), ,
,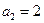 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,试问是否存在
,试问是否存在 ,使对任意的
,使对任意的 都有
都有 成立,若存在,求出
成立,若存在,求出 的取值范围;不存在, 说明理由;
的取值范围;不存在, 说明理由;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三第一学期期中考试试题数学 题型:解答题
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
对于数列 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 称作周期为
称作周期为 的周期数列,
的周期数列, 的最小值称作数列
的最小值称作数列 的最小正周期,以下简称周期。例如当
的最小正周期,以下简称周期。例如当 时
时 是周期为
是周期为 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。
(1)设数列 满足
满足 (
( ),
), (
(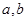 不同时为0),且数列
不同时为0),且数列 是周期为
是周期为 的周期数列,求常数
的周期数列,求常数 的值;
的值;
(2)设数列 的前
的前 项和为
项和为 ,且
,且 .
.
①若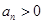 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列 满足
满足 (
( ),
),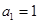 ,
,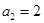 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,试问是否存在
,试问是否存在 ,使对任意的
,使对任意的 都有
都有 成立,若存在,求出
成立,若存在,求出 的取值范围;不存在,
说明理由;
的取值范围;不存在,
说明理由;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市十三校高三上学期第一次联考试题文科数学 题型:解答题
(本题满分18分,第1小题满分5分,第2小题满分5分,第3小题满分8分)
已知函数 ,其中
,其中 .
.
(1)当 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域;
(2)当 ,
, 时,求
时,求 的最小值;
的最小值;
(3)设 ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年上海市徐汇区高三第二次模拟考试数学卷(文) 题型:解答题
(本题满分18分;第(1)小题5分,第(2)小题5分,第(3)小题8分)
设数列 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列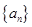 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
(1)若 ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”;
(2)试判断数列 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么?
(3)设 是数列
是数列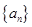 的前
的前 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求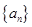 的通项公式,若不存在,说明理由.
的通项公式,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com