
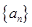 满足:
满足: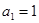 ,
,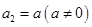 ,
,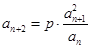 (其中
(其中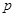 为非零常数,
为非零常数,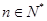 ).
).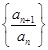 是不是等比数列?
是不是等比数列?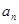 ;
;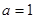 时,令
时,令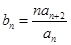 ,
,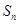 为数列
为数列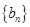 的前
的前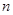 项和,求
项和,求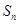 .
.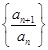 是等比数列;(2)
是等比数列;(2)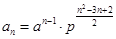 ,
,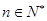 ;(3)
;(3)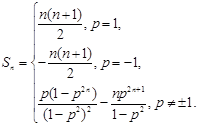 .
.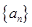 的递推式
的递推式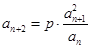 进行变形得
进行变形得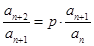 ,从而利用定义得到数列
,从而利用定义得到数列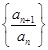 是等比数列;(2)在(1)的基础上先求出数列
是等比数列;(2)在(1)的基础上先求出数列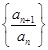 的通项公式,再利用累乘法求数列
的通项公式,再利用累乘法求数列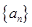 的通项公式;(3)在(2)的基础上,将
的通项公式;(3)在(2)的基础上,将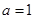 代入数列
代入数列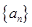 的通项公式,从而求出数列
的通项公式,从而求出数列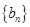 的通项公式,并根据数列
的通项公式,并根据数列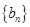 的通项公式
的通项公式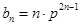 ,对
,对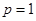 、
、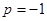 以及
以及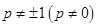 进行三种情况的分类讨论,前两种情况利用等差数列求和即可,在最后一种情况下利用错位相减法求数列
进行三种情况的分类讨论,前两种情况利用等差数列求和即可,在最后一种情况下利用错位相减法求数列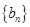 的前
的前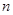 项和
项和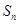 ,最后用分段的形式表示数列
,最后用分段的形式表示数列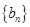 的前
的前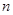 项和
项和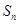 .
.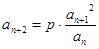 ,得
,得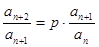 .
. 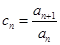 ,则
,则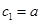 ,
, .
.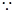
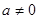 ,
,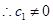 ,
,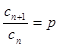 (非零常数),
(非零常数),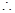 数列
数列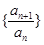 是等比数列.
是等比数列.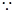 数列
数列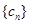 是首项为
是首项为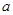 ,公比为
,公比为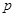 的等比数列,
的等比数列,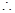
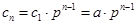 ,即
,即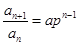 .
.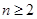 时,
时,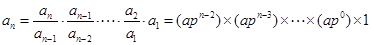
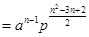 ,
,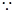
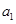 满足上式,
满足上式,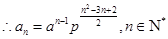 .
.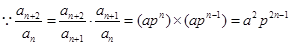 ,
,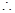 当
当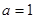 时,
时,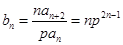 .
.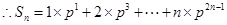 , ①
, ①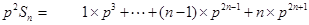 ②
②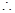 当
当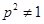 ,即
,即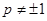 时,①
时,①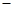 ②得:
②得: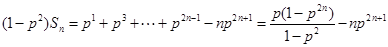 ,
,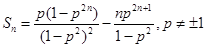 .
.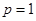 时,
时,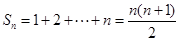 ,
,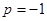 时,
时,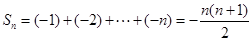 .
. 


科目:高中数学 来源:不详 题型:解答题
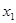 (
(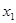 =100万辆),第
=100万辆),第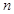 年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为
年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为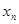 ,该年的增长量
,该年的增长量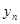 和
和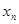 与
与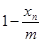 的乘积成正比,比例系数为
的乘积成正比,比例系数为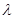
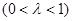 其中
其中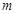 =200万.
=200万.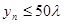 ;
;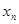 表示
表示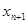 ;并说明该市汽车总拥有量是否能控制在200万辆内.
;并说明该市汽车总拥有量是否能控制在200万辆内.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
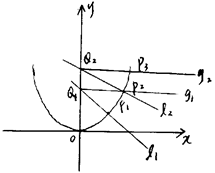
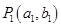 是曲线C:
是曲线C: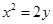 上的一点(其中
上的一点(其中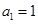 ),过点
),过点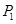 作与曲线C在
作与曲线C在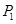 处的切线垂直的直线
处的切线垂直的直线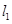 交
交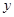 轴于点
轴于点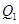 ,过
,过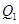 作与
作与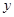 轴垂直的直线
轴垂直的直线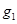 与曲线C在第一象限交于点
与曲线C在第一象限交于点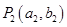 ;再过点
;再过点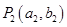 作与曲线C在
作与曲线C在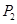 处的切线垂直的直线
处的切线垂直的直线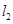 交轴于点
交轴于点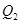 ,过
,过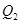 作与
作与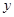 轴垂直的直线
轴垂直的直线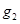 与曲线C在第一象限交于点
与曲线C在第一象限交于点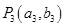 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点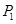 、
、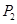 、、
、、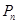 、。(其中
、。(其中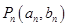 )
)
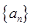 的通项公式。
的通项公式。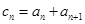 ,且
,且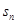 是数列
是数列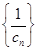 的前
的前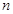 项和,
项和,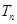 是数列
是数列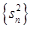 的前
的前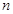 项
项查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com