
分析 通过设点T的坐标可知直线AB的方程,联立直线AB与椭圆方程利用韦达定理、两点间距离公式及中点坐标公式可知相等AB的长度及点Q的坐标,进而可得弦AB的中垂线方程,从而可知点P坐标,利用三角形面积公式计算即得结论.
解答 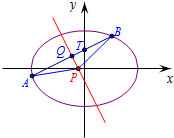 解:依题意,设T(0,t),则直线AB方程为:x-2y+2t=0,
解:依题意,设T(0,t),则直线AB方程为:x-2y+2t=0,
联立直线AB与椭圆方程,消去x整理得:3y2-4ty+2t2-1=0,
由韦达定理可知:y1+y2=$\frac{4}{3}$t,y1y2=$\frac{2{t}^{2}-1}{3}$,
∴x1+x2=2(y1+y2)-4t=$\frac{8}{3}$t-4t=-$\frac{4}{3}$t,
则|AB|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
=$\sqrt{5}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{5}$•$\sqrt{\frac{16{t}^{2}}{9}-\frac{8{t}^{2}-4}{3}}$
=$\frac{2\sqrt{5}}{3}$•$\sqrt{3-2{t}^{2}}$,
由中点坐标公式可知点Q($\frac{4}{3}$-2t,$\frac{2}{3}$t),
故弦AB的中垂线方程为:2x+y+$\frac{10}{3}$t-$\frac{8}{3}$=0,
∴点P坐标为P($\frac{4}{3}$-$\frac{5}{3}$t,0),
∴|PQ|=$\sqrt{[(\frac{4}{3}-\frac{5}{3}t)-(\frac{4}{3}-2t)]^{2}+(0-\frac{2}{3}t)^{2}}$=$\frac{\sqrt{5}}{3}$|t|,
∴S△PAB=$\frac{1}{2}$•|PQ|•|AB|
=$\frac{1}{2}$•$\frac{\sqrt{5}}{3}$|t|•$\frac{2\sqrt{5}}{3}$•$\sqrt{3-2{t}^{2}}$
=$\frac{5}{9}$•$\sqrt{-2({t}^{2}-\frac{3}{4})^{2}+\frac{9}{8}}$,
∴当t2=$\frac{3}{4}$时,S△PAB取最大值$\frac{5}{9}$•$\sqrt{\frac{9}{8}}$=$\frac{5\sqrt{2}}{12}$,
∴△PAB面积的最大值为$\frac{5\sqrt{2}}{12}$.
点评 本题是一道直线与圆锥曲线的综合题,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 5 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(\frac{1}{2}x+\frac{π}{12})$ | B. | $y=sin(\frac{1}{2}x-\frac{π}{12})$ | C. | $y=sin(2x+\frac{π}{12})$ | D. | $y=sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 成绩分组 | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 5 | 15 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-2,3] | C. | (-3,1) | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|22k-1<x<22k,k∈Z} | B. | {x|22k<x<22k+1,k∈Z} | ||
| C. | {x|22k-1<x<22k+1,k∈Z} | D. | {x|22k<x<22k+2,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com