
一个平面用
n条直线去划分,最多能被分成几块?此问题可以推广到空间吗?若能,试解答此空间的问题.|
解:方法一: (归纳法)当这些直线互不平行且没有两条以上的直线交于同一点时,才能使分成的块数最多.当 n=1,2,3,4,5时,平面被分成的块数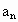 分别是: 分别是: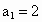 , ,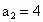 , ,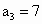 , ,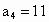 , ,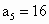 ,如果只是从这5个数字来寻找规律,是比较困难的.可以从一条直线划分平面开始,逐条增加,寻求块数的增加规律,如下图所示. ,如果只是从这5个数字来寻找规律,是比较困难的.可以从一条直线划分平面开始,逐条增加,寻求块数的增加规律,如下图所示.
平面块数: 2+1+l=2+2 4+1+2=4+37 +2+2=7+4 11+3+2=11+5每增加一条直线 l,l都要与前面的n-1条直线相交,增加的平面块数是n块,即(n-1)+1=n.其中有一个常数2,即增加的平面的块数可以看作是与n-2条直线是一致的,与另一条直线相交时增加2块.尝试在上面的块数中分出一个常数2以及块数中找到总的直线的条数n,则:2=1 +2+(-1),2+2=2+2,4+3=2+3+2,7+4=4+5+2,11+5=9+5+2,而2要写成三个数相加的形式,则还缺数值,显然加上一个数不好寻找,可以尝试增加倍数,例如乘以2,可得:
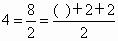 , ,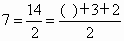 , ,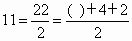 , ,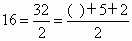 ,括号内的数值分别是l,4,9,16,25,恰好为完全平方数,所以可以猜想: ,括号内的数值分别是l,4,9,16,25,恰好为完全平方数,所以可以猜想: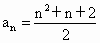 . .
方法二:设 n-1条直线把平面分成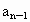 块,现在我们再添加第n条直线,它与前面n-1条直线都相交,增加的平面块数恰好为n块. 块,现在我们再添加第n条直线,它与前面n-1条直线都相交,增加的平面块数恰好为n块.
所以当 n=1,2,…,n时, 即 即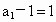 , ,
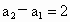 . .
…… ……
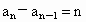 . .
所以  ,即 ,即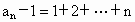 , ,
所以 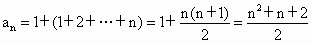 . .
因此一个平面用 n条直线去划分,最多被分成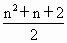 块. 块.
类比平面几何中的问题,可以得到空间的平面划分空间的块数的问题: 一个空间用 n个平面去划分,最多能被分成几部分?显然,在空间中,当且仅当以下情况时,产生的空间块数最多: (1)三个或三个以上的平面产生的交线互不平行;(2)四个以上平面不能交于一点.考虑增加一个平面,可以把空间划分的块数所增加的数.由于第 n个平面与前n-1个平面都相交,则在第n个平面上就有n-1条交线,那么第n个平面被这n-1条交线分成的平面块数是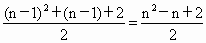 ,而每个平面块把它所在的那个空间块一分为二,于是增加了 ,而每个平面块把它所在的那个空间块一分为二,于是增加了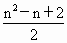 个空间块,所以空间被n个平面划分成的块数 个空间块,所以空间被n个平面划分成的块数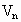 与空间被n-1个平面划分成的块数 与空间被n-1个平面划分成的块数 的关系是: 的关系是: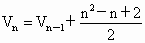 . .
令 n=1,2,…,n,则:
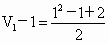 . .
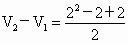 . .
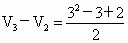 . .
…… ……
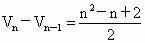 . .
把以上 n个等式相加得:
故一个空间用 n个平面去划分,最多能被分成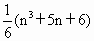 个空间块. 个空间块. |


科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修1-2) 2009-2010学年 第39期 总第195期 北师大课标 题型:044
一个平面用n条直线去划分,最多将平面分成f(n)个部分.
(1)求f(1),f(2),f(3),f(4);
(2)观察f(2)-f(1),f(3)-f(2),f(4)-f(3)有何规律;
(3)求出f(n).
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修1-2 2.1合情推理与演绎推理练习卷(解析版) 题型:解答题
一个平面用n条直线去划分,最多将平面分成 个部分.
个部分.
(1)求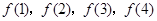 ;
;
(2)观察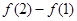 ,
,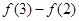 ,
, 有何规律;
有何规律;
(3)求出
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com