
设数列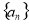 为等差数列,且
为等差数列,且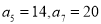 ,数列
,数列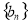 的前
的前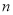 项和为
项和为 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前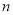 项和
项和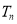 .
.
(1)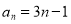 ,
,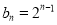 ;(2)
;(2)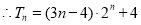
【解析】
试题分析: (1)由等差数列的通项公式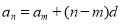 求公差
求公差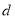 ,即可求
,即可求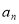 ;利用
;利用 ,求
,求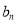 ;(2)
;(2)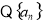 是等差数列,
是等差数列,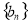 是等比数列,
是等比数列,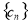 是由两者相乘,
是由两者相乘, 利用错位相减法求和即可.规律总结:1.等差数列的求解问题,要抓住五个基本量(
利用错位相减法求和即可.规律总结:1.等差数列的求解问题,要抓住五个基本量(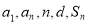 ),一般题型是“知三求二”,利用方程思想(关于
),一般题型是“知三求二”,利用方程思想(关于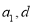 的方程)进行求有关量;2对于
的方程)进行求有关量;2对于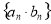 (其中
(其中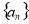 是等差数列,
是等差数列,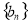 是等比数列)的求和问题,要利用错位相减法(乘公比
是等比数列)的求和问题,要利用错位相减法(乘公比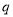 后,错位相减).
后,错位相减).
注意点:错位相减法,一定要向后错一位,使同次数的项对齐,以便正确化简;一定要搞清相减后,有多少项可构成等比数列.
试题解析: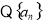 是等差数列,
是等差数列,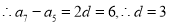
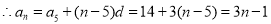
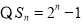 ,
, 当
当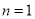 时,
时,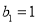 ;当
;当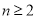 时,
时,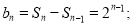
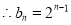 .
.
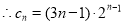
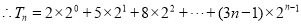

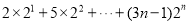
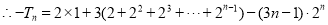
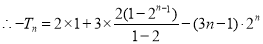
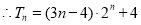
考点:1.等差数列;2.等比数列;3.错位相减法求数列的前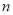 项和.
项和.


科目:高中数学 来源:2016届甘肃省高一下学期期中考试数学试卷(解析版) 题型:选择题
已知x与y之间的几组数据如下表:
x | 0 | 1 | 2 | 3 |
y | 0 | 2 | 6 | 7 |
则y与x的线性回归方程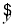 =
=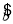 x+
x+ 必过点( )
必过点( )
A.(1,2) B.(2,6) C.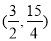 D.(3,7)
D.(3,7)
查看答案和解析>>
科目:高中数学 来源:2016届湖南省高一下学期6月五科联赛数学试卷(解析版) 题型:选择题
在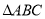 中的内角
中的内角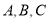 所对的边分别为
所对的边分别为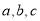 ,若
,若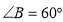
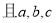 成等比数列,则
成等比数列,则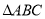 的形状为
的形状为
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 不确定
查看答案和解析>>
科目:高中数学 来源:2016届湖南省益阳市高一下学期期中考试数学试卷(解析版) 题型:选择题
已知tan(α+β)=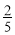 ,tan(α+
,tan(α+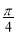 )=
)=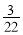 , 那么tan(β-
, 那么tan(β-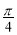 )的值是( )
)的值是( )
A.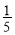 B.
B.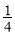 C.
C.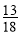 D.
D.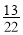
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com