
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() 使得平面
使得平面![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先利用平面几何知识证明![]() ,利用平面
,利用平面![]() 平面
平面![]() 的性质可证明
的性质可证明![]() 平面
平面![]() ;(2)作
;(2)作![]() 与底面垂直,以
与底面垂直,以![]() 为坐标轴建立空间直角坐标系,利用向量垂直数量积为零列方程求出平面
为坐标轴建立空间直角坐标系,利用向量垂直数量积为零列方程求出平面![]() 的一个法向量,利用向量的夹角公式,即可求
的一个法向量,利用向量的夹角公式,即可求![]() 和平面
和平面![]() 所成角的正弦值;(3)求出平面
所成角的正弦值;(3)求出平面![]() —个法向量,利用平面
—个法向量,利用平面![]() 平面
平面![]() ,法向量的数量积为0 ,即可得出结论.
,法向量的数量积为0 ,即可得出结论.
(1)证明:由BC⊥CD,BC=CD=2,可得![]() .
.
由EA⊥ED,且EA=ED=2,可得![]() .又AB=4,所以BD⊥AD.
.又AB=4,所以BD⊥AD.
又平面EAD⊥平面ABCD,平面ADE∩平面ABCD=AD,BD平面ABCD,
所以BD⊥平面ADE.
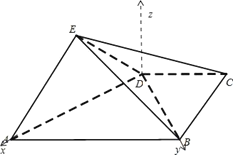
(2)解:建立空间直角坐标系D﹣xyz,
则D(0,0,0),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() =(x,y,z)是平面CDE的一个法向量,则
=(x,y,z)是平面CDE的一个法向量,则![]() 令x=1,则
令x=1,则![]() =(1,1,﹣1).
=(1,1,﹣1).
设直线BE与平面CDE所成的角为α,则sinα=![]()
所以BE和平面CDE所成的角的正弦值![]() .
.
(3)解:设![]() ,λ∈[0,1].
,λ∈[0,1].
![]() ,
,![]() ,
,
![]() .则
.则![]() .
.
设![]() =(x',y',z')是平面BDF一个法向量,则
=(x',y',z')是平面BDF一个法向量,则![]()
令x'=1,则![]() =(1,0,﹣
=(1,0,﹣![]() ).
).
若平面BDF⊥平面CDE,则![]()
![]() =0,即
=0,即![]() ,
,![]() .
.
所以,在线段CE上存在一点F使得平面BDF⊥平面CDE.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系xOy的原点为极点,x轴的非负半轴为极轴建立极坐标系,且两坐标系相同的长度单位.已知点N的极坐标为( ![]() ,
, ![]() ),M是曲线C1:ρ=1上任意一点,点G满足
),M是曲线C1:ρ=1上任意一点,点G满足 ![]() ,设点G的轨迹为曲线C2 .
,设点G的轨迹为曲线C2 .
(1)求曲线C2的直角坐标方程;
(2)若过点P(2,0)的直线l的参数方程为  (t为参数),且直线l与曲线C2交于A,B两点,求
(t为参数),且直线l与曲线C2交于A,B两点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的编号为003.这600名学生分住在3个营区,从001到300住在第1营区,从301到495住在第2营区,从496到600住在第3营区,则3个营区被抽中的人数依次为( )
A. 26,16,8 B. 25,16,9
C. 25,17,8 D. 24,17,9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.则获得复赛资格的人数为( )
内,其频率分布直方图如图.则获得复赛资格的人数为( )

A. 520 B. 540 C. 620 D. 640
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com