
【题目】设函数f(x)=| ![]() ﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
A.(﹣∞,0]
B.(﹣∞,1]
C.(﹣∞,2]
D.(﹣∞,3]
【答案】D
【解析】解:对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥mm≤f(x)max,x∈[1,4].
令u(x)= ![]() ﹣ax,∵a>0,∴函数u(x)在x∈[1,4]单调递减,
﹣ax,∵a>0,∴函数u(x)在x∈[1,4]单调递减,
∴u(x)max=u(1)=4﹣a,u(x)min=1﹣a.①a≥4时,0≥4﹣a>1﹣a,则f(x)max=a﹣1≥3.②4>a>1时,4﹣a>0>1﹣a,则f(x)max={4﹣a,a﹣1}max<3.③a≤1时,4﹣a>1﹣a≥0,则f(x)max=4﹣a≥3.
综上①②③可得:m≤3.
∴实数m的取值范围为(﹣∞,3].
故选:D.
【考点精析】通过灵活运用函数的最值及其几何意义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx+2 ![]() cosωxsinωx+sin(ωx+
cosωxsinωx+sin(ωx+ ![]() )sin(ωx﹣
)sin(ωx﹣ ![]() )(ω>0),且f(x)的最小正周期为π.
)(ω>0),且f(x)的最小正周期为π.
(1)求ω的值;
(2)求函数f(x)在区间(0,π)上的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(﹣ ![]() ,
, ![]() ),∠AOB=α.
),∠AOB=α. 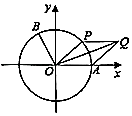
(1)求 ![]() 的值;
的值;
(2)设∠AOP=θ( ![]() ≤θ≤
≤θ≤ ![]() ),
), ![]() =
= ![]() +
+ ![]() ,四边形OAQP的面积为S,f(θ)=(
,四边形OAQP的面积为S,f(θ)=( ![]()
![]() ﹣
﹣ ![]() )2+2S2﹣
)2+2S2﹣ ![]() ,求f(θ)的最值及此时θ的值.
,求f(θ)的最值及此时θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义min{a,b}= ![]() ,若函数f(x)=min{x2﹣3x+3,﹣|x﹣3|+3},且f(x)在区间[m,n]上的值域为[
,若函数f(x)=min{x2﹣3x+3,﹣|x﹣3|+3},且f(x)在区间[m,n]上的值域为[ ![]() ,
, ![]() ],则区间[m,n]长度的最大值为( )
],则区间[m,n]长度的最大值为( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
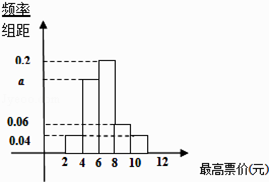
【题目】2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下: (Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价 | 35岁以下人数 |
[2,4) | 2 |
[4,6) | 8 |
[6,8) | 12 |
[8,10) | 5 |
[10,12] | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组中的函数f(x),g(x)表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=x+1,g(x)= ![]()
C.f(x)=|x|,g(x)= ![]()
D.f(x)=log22x , g(x)=2log2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com