
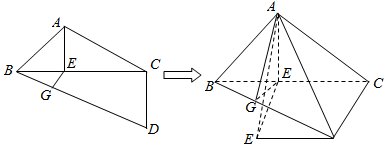
 一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.
一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.分析 (1)根据面面垂直的判定定理即可证明平面ABD⊥平面ACD;
(2)根据异面直线所成角的定义进行转化即可求AD与BC所成的角的正切值;
(3)根据二面角的定义作出二面角的平面角即可求二面角A-BD-C的大小的正切值.
解答 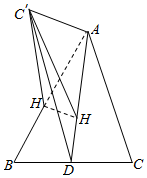 (1)证明:取BC中点E,连结AE,∵AB=AC,∴AE⊥BC
(1)证明:取BC中点E,连结AE,∵AB=AC,∴AE⊥BC
∵平面ABC⊥平面BCD,∴AE⊥平面BCD,
∵BC⊥CD,由三垂线定理知AB⊥CD.
又∵AB⊥AC,∴AB⊥平面BCD,∵AB?平面ABD.
∴平面ABD⊥平面ACD.
(2)解:在面BCD内,过D作DF∥BC,过E作EF⊥DF,交DF于F,由三垂线定理知AF⊥DF,∠ADF为AD与BC所成的角.
设AB=m,则BC=$\sqrt{2}$m,CE=DF=$\frac{{\sqrt{2}}}{2}$m,CD=EF=$\frac{{\sqrt{6}}}{3}$m∴$tanADF=\frac{AF}{DF}=\frac{{\sqrt{A{E^2}+E{F^2}}}}{DF}=\frac{{\sqrt{21}}}{3}$,
即AD与BC所成的角的正切值为$\frac{{\sqrt{21}}}{3}$.
(3)解:∵AE⊥面BCD,过E作EG⊥BD于G,连结AG,由三垂线定理知AG⊥BD,
∴∠AGE为二面角A-BD-C的平面角
∵∠EBG=30°,BE=$\frac{{\sqrt{2}}}{2}$m,∴EG=$\frac{{\sqrt{2}}}{4}$m
又AE=$\frac{{\sqrt{2}}}{2}$m,∴tanAGE=$\frac{AE}{GE}$=2,即二面角A-BD-C的大小的正切值为2.
点评 本题主要考查面面垂直的判断以及空间二面角和异面直线所成角的求解,根据空间角的定义进行转化是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
在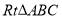 中,
中,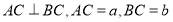 ,则
,则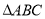 的外接圆半径
的外接圆半径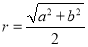 ;类比到空间,若三棱锥
;类比到空间,若三棱锥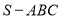 的三条侧棱
的三条侧棱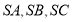 两两互相垂直,且长度分别为
两两互相垂直,且长度分别为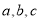 ,则三棱锥
,则三棱锥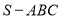 的外接球的半径
的外接球的半径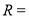 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
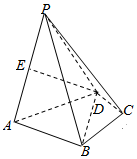 如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.
如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
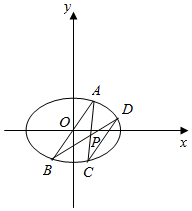 如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.
如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com