已知数列{an},{bn}分别是等差数列和等比数列,且a2=b2=2,a4=b4=8.
(1)求数列{an},{bn}的通项an,bn.
(2)求数列{an},{bn}的前n项和Sn,Tn.
解:(1)设等差数列{a
n}的公差为d,等比数列{b
n}的公比为q,
由题意可得
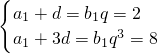
,解得a
1=-1,d=3,
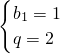
或
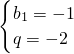
,
故由等差数列的通项公式可得a
n=-1+3(n-1)=3n-4,
由等比数列的求和公式可得b
n=1•2
n-1=2
n-1,或b
n=(-1)(-2)
n-1=-(-2)
n-1;
(2)由(1)可知a
n=3n-4,b
n=2
n-1,或b
n=-(-2)
n-1;
由等差数列的求和公式可得:S
n=
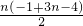
=
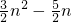
,
由等差数列的求和公式可得当b
n=2
n-1时,T
n=
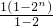
=2
n-1,
当b
n=-(-2)
n-1时,T
n=
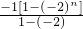
=
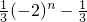
分析:(1)设等差数列{a
n}的公差为d,等比数列{b
n}的公比为q,由题意可得关于首项和公差,公比的方程组,解之可得通项公式;
(2)由(1)可知通项公式,进而可得数列的前n项和公式.
点评:本题考查等差数列和等比数列的通项公式和求和公式,属中档题.

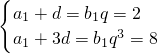 ,解得a1=-1,d=3,
,解得a1=-1,d=3,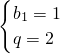 或
或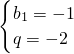 ,
,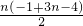 =
=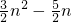 ,
,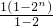 =2n-1,
=2n-1,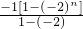 =
=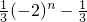


 阅读快车系列答案
阅读快车系列答案