Question

1．已知定义在R上的偶函数f（x）满足对任意x∈R都有f（x+4）=f（x），且当x∈[-2，0]时，$f（x）={（\frac{1}{2}）^x}-1$．若在区间x∈（-2，6）内函数g（x）=f（x）-log_a（x+2）有3个不同的零点，则实数a的取值范围为（$\root{3}{4}$，2）．

Answer 1

分析 由题意可得，分别画出y=f（x）和y=log_a（x+2）的图象，数形结合求得a的范围．

解答 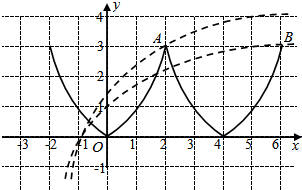解：∵偶函数f（x）满足对任意x∈R都有f（x+4）=f（x），
∴函数f（x）的周期为4，
当x∈[-2，0]时，$f（x）={（\frac{1}{2}）^x}-1$，
∴x∈[0，2]时，f（x）=2^x-1，
分别画出y=f（x）和y=log_a（x+2）的图象，
在区间x∈（-2，6）内，
如图所示，函数y=log_a（x+2）的图象过定点（-1，0），
当y=log_a（x+2）的图象可点A时，即3=log_a（2+2），即a=$\root{3}{4}$时，有2个零点，
当y=log_a（x+2）的图象可点B时，即3=log_a（2+6），即a=2，有3个零点，
∵在区间x∈（-2，6）内函数g（x）=f（x）-log_a（x+2）有3个不同的零点，
∴$\root{3}{4}$＜a≤2，
故a的取值范围为（$\root{3}{4}$，2]，
故答案为：（$\root{3}{4}$，2]．

点评 本题主要考查函数的零点与方程的根的关系，体现了转化、数形结合的数学思想，属于中档题．