练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．某校从6名教师中选派3名教师同时去3个贫困地区支教，每个地区1人，其中甲和乙不同去，甲和丙只能同去或同不去，则不同的选派方案有（　　）
    A．24种B．42种C．36种D．48种

    分析 先从6名教师中选出3名，因为甲和乙不同去，甲和丙只能同去或同不去，所以可按选甲和不选甲分成两类，两类方法数相加，再把3名老师分配去3个边远地区支教，3名教师进行全排列即可．

    解答 解：根据题意，分两步进行分析：
    ①、先从6名教师中选出三名老师，
    又分需分2类进行讨论
    1、甲去，则丙一定去，乙一定不去，有C31=3种不同选法
    2、甲不去，则丙一定不去，乙可能去也可能不去，有C43=4种不同选法，
    ∴不同的选法有3+4=7种
    ②、将选出的三名老师全排列，对应3个地区，有A33=6种情况，
    根据分步计数原理得不同的选派方案共有，7×6=42．
    故选：B．

    点评 本题考查了排列组合的综合应用，关键是审清题意，明确条件、事件之间的关系，要分清用排列还是用组合去做．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=3sin（2x+$\frac{π}{6}$）．
    （1）求函数f（x）的周期；
    （2）求函数f（x）的单调增区间；
    （3）当x取何值时，f（x）有最大值，最大值为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．将y=sin（2x-$\frac{π}{6}$）图象向右平移$\frac{π}{12}$个单位，所得函数图象的一条对称轴的方程是（　　）
    A．x=$\frac{π}{12}$B．x=$\frac{π}{6}$C．x=$\frac{π}{3}$D．x=-$\frac{π}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知定义在R上的偶函数f（x）满足对任意x∈R都有f（x+4）=f（x），且当x∈[-2，0]时，$f（x）={（\frac{1}{2}）^x}-1$．若在区间x∈（-2，6）内函数g（x）=f（x）-loga（x+2）有3个不同的零点，则实数a的取值范围为（$\root{3}{4}$，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知（x+1）n=a0+a1（x-1）+a2（x-1）2+…+an（x-1）n，（其中n∈N*）．
    （1）求a0及sn=a1+a2+…+an；
    （2）试比较sn与（n-2）•2n+2n2的大小，并用数学归纳法给出证明过程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．在△ABC中，A，B，C所对的边分别为a，b，c，有$\sqrt{3}$acosC-csinA=0．
    （Ⅰ）求角C的大小；
    （Ⅱ）若$a=\sqrt{13}$，S△ABC=3$\sqrt{3}$，求b，c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

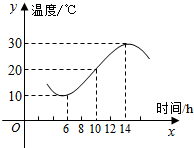    5．如图，某地一天从6时到14时的温度变化曲线近似满足函数f（x）=Asin（ωx+φ）+b，（A＞0，ω＞0，0＜φ＜π）．
    （1）写出这段曲线的函数f（x）的解析式；
    （2）当x∈R时，若函数g（x）=f（x+m）是偶函数，求实数|m|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．5+12i的平方根3+2i或-3-2i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．如图是“推理与证明”的知识结构图，如果要加入“归纳”，则应该放在（　　）
    A．“合情推理”的下位B．“演绎推理”的下位
    C．“直接证明”的下位D．“间接证明”的下位

    查看答案和解析>>

    同步练习册答案