
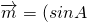 ,sinB),
,sinB),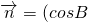 ,cosA),
,cosA),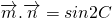 且A,B,C分别为的三边a,b,c的角.
且A,B,C分别为的三边a,b,c的角.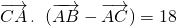 ,求边c的长.
,求边c的长.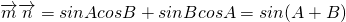
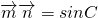
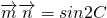 ,
, ,又C∈(0,π)
,又C∈(0,π) ;
;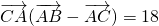 ,
,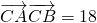 ,
,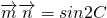 ,得到sin2C等于sinC,化简后即可求出cosC的值,根据C的范围,利用特殊角的三角函数值即可求出C的度数;
,得到sin2C等于sinC,化简后即可求出cosC的值,根据C的范围,利用特殊角的三角函数值即可求出C的度数;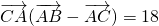 ,利用平面向量的数量积的运算法则得到ab的值,利用余弦定理表示出c的平方,把求出的C的度数,a+b=2c及ab的值代入即可列出关于c的方程,求出方程的解即可得到c的值.
,利用平面向量的数量积的运算法则得到ab的值,利用余弦定理表示出c的平方,把求出的C的度数,a+b=2c及ab的值代入即可列出关于c的方程,求出方程的解即可得到c的值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| 2π |
| 3 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知向量![]() =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量![]() (2,0)所成角为
(2,0)所成角为![]() ,其中A, B, C是⊿ABC的内角.
,其中A, B, C是⊿ABC的内角.
(1)求角B的大小; (2)求sinA+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省福州市三山中学高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
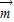 =(sinB,1-cosB),向量
=(sinB,1-cosB),向量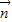 =(2,0),且
=(2,0),且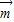 与
与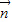 的夹角为
的夹角为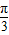 ,
,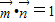 其中A,B,C是△ABC的内角.
其中A,B,C是△ABC的内角.查看答案和解析>>
科目:高中数学 来源:2008-2009学年浙江省杭州高级中学高三第三次月考数学试卷(文科)(解析版) 题型:解答题
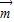 =(sinB,1-cosB),向量
=(sinB,1-cosB),向量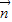 =(2,0),且
=(2,0),且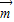 与
与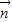 的夹角为
的夹角为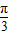 ,
, 其中A,B,C是△ABC的内角.
其中A,B,C是△ABC的内角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com