
已知函数 的图象在点
的图象在点 处的切线恰好与直线
处的切线恰好与直线 平行,若
平行,若 在区间
在区间 上单调递减,则实数
上单调递减,则实数 的取值范围是
的取值范围是
A. B.
B. C.
C. D.
D.
B
【解析】
试题分析:解:∵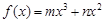 ,∴f’(x)=-3mx2+2nx,∴f’(-1)=-3m-2n,∵函数
,∴f’(x)=-3mx2+2nx,∴f’(-1)=-3m-2n,∵函数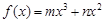 的图象在点(-1,2)处的切线恰好与直线3x+y=0平行,∴-3m-2n=-3,m+n=2,,解得m=-1,n=3,∴f’(x)=3x2+6x,令f’(x)=3x2+6x≤0,解得-2≤x≤0,∴函数f(x)在[-2,0]上单调递减,∵f(x)在区间[t,t+1]上单调递减,∴
的图象在点(-1,2)处的切线恰好与直线3x+y=0平行,∴-3m-2n=-3,m+n=2,,解得m=-1,n=3,∴f’(x)=3x2+6x,令f’(x)=3x2+6x≤0,解得-2≤x≤0,∴函数f(x)在[-2,0]上单调递减,∵f(x)在区间[t,t+1]上单调递减,∴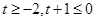 ,解得
,解得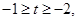 故选B.
故选B.
考点:导数的几何意义,函数单调性
点评:本题考查利用导数求曲线上某点处的切线方程的应用,具体涉及到导数的几何意义、直线平行的条件、利用导数判断函数的单调等知识点,解题时要认真审题,仔细解答


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2012-2013学年福建省高三5月月考文科数学试卷(解析版) 题型:解答题
已知函数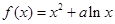 的图象在点
的图象在点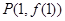 处的切线斜率为
处的切线斜率为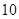 .
.
(Ⅰ)求实数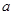 的值;
的值;
(Ⅱ)判断方程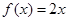 根的个数,证明你的结论;
根的个数,证明你的结论;
(Ⅲ)探究:是否存在这样的点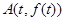 ,使得曲线
,使得曲线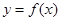 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届山西省高二第二学期3月月考理科数学试卷 题型:选择题
已知函数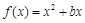 的图象在点
的图象在点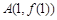 处的切线的斜率为3,数列
处的切线的斜率为3,数列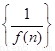
的前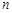 项和为
项和为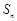 ,则
,则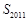 的值为( )
的值为( )
A、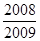 B、
B、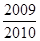 C、
C、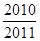 D、
D、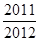
查看答案和解析>>
科目:高中数学 来源:2010年福建省八县(市高二下学期期末联考(文科)数学卷 题型:解答题
(本题满分14分)已知函数 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且在
,且在 处取得极小值。
处取得极小值。
(1)求 的解析式;
的解析式;
(2)已知函数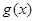 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间 ,使得
,使得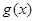 在
在 的值域也是
的值域也是 ,称区间
,称区间 为函数
为函数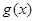 的“保值区间”.
的“保值区间”.
①当 时,请写出函数
时,请写出函数 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明);
②当 时,问
时,问 是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com