
分析 对四个选项分别进行判断,即可得出结论.
解答 解:①∵a=1,b=$\sqrt{3}$,A=30°,
∴$\frac{1}{sin30°}=\frac{\sqrt{3}}{sinB}$,
∴sinB=$\frac{\sqrt{3}}{2}$,
∵b>a,
∴B>A,
∴B=60°或120°,故不正确;
②由①可知△ABC的面积有2个值,故不正确;
③设△ABC外接圆的半径为R,则2R=$\frac{1}{sin30°}$=2,∴R=1,∴△ABC外接圆的面积为π,故不正确;
④由②可知,△ABC内切圆的半径有两个值.
故答案为:0.
点评 本题考查正弦定理的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=x-2 | B. | y=x-2(0≤y≤1) | C. | y=x+2(-2≤x≤-1) | D. | y=x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
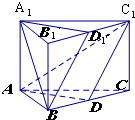 如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.
如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {锐角三角形} | B. | {钝角三角形} | C. | {直角三角形} | D. | {三角形} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com