
已知函数![]() .
.
(Ⅰ)当![]() 时,证明函数
时,证明函数![]() 只有一个零点;
只有一个零点;
(Ⅱ)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围
的取值范围
(Ⅱ)![]()
(Ⅰ)当![]() 时,
时,![]() ,其定义域是
,其定义域是![]()
∴ ![]() …………2分
…………2分
令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
![]() ,∴
,∴ ![]() 舍去.
舍去.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴ 函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减
上单调递减
∴ 当x =1时,函数![]() 取得最大值,其值为
取得最大值,其值为![]() .
.
当![]() 时,
时,![]() ,即
,即![]() .
.
∴ 函数![]() 只有一个零点. ……………………6分
只有一个零点. ……………………6分
(Ⅱ)显然函数![]() 的定义域为
的定义域为![]()
∴ ![]() ………7分
………7分
①当![]() 时,
时,![]() 在区间
在区间![]() 上为增函数,不合题意……8分
上为增函数,不合题意……8分
② 当![]() 时,
时,![]() 等价于
等价于![]() ,即
,即![]()
此时![]() 的单调递减区间为
的单调递减区间为![]() .
.
依题意,得![]() 解之得
解之得![]() . ………10分
. ………10分
③ 当![]() 时,
时,![]() 等价于
等价于![]() ,即
,即![]()
此时![]() 的单调递减区间为
的单调递减区间为![]() ,
,
∴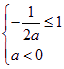 得
得![]()
综上,实数![]() 的取值范围是
的取值范围是![]() …………12分
…………12分
法二:
①当![]() 时,
时,![]() 在区间
在区间![]() 上为增函数,不合题意……8分
上为增函数,不合题意……8分
②当![]() 时,要使函数
时,要使函数![]() 在区间
在区间![]() 上是减函数,只需
上是减函数,只需![]() 在区间
在区间
![]() 上恒成立,
上恒成立,![]()
![]() 只要
只要![]() 恒成立,
恒成立,
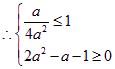 解得
解得![]() 或
或![]()
综上,实数![]() 的取值范围是
的取值范围是![]() …………12分
…………12分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com