
【题目】某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.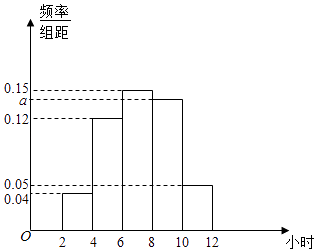
(1)求这100名学生中参加实践活动时间在6~10小时内的人数;
(2)估计这100名学生参加实践活动时间的众数、中位数和平均数.
【答案】
(1)【解答】解:依题意,100名学生中参加实践活动的时间在6~10小时内的人数为:
100×[1﹣(0.04+0.12+0.05)×2]=58,
即这100名学生中参加实践活动时间在6~10小时内的人数为58.
(2)【解答】解:由频率分布直方图可以看出最高矩形横轴上的中点为7,
故这100名学生参加实践活动时间的众数的估计值为7小时,
由(0.04+0.12+0.15+a+0.05)×2=1,解得a=0.14,
则6+ ![]() ,
,
即这100名学生参加实践活动时间的中位数为7.2小时,
这100名学生参加实践活动时间的平均数为:
0.04×2×3+0.12×2×5+0.15×2×7+0.14×2×9+0.05×2×11=7.16小时.
【解析】(1)利用频率分布直方图能求出100名学生中参加实践活动的时间在6~10小时内的人数.
(2)由频率分布直方图可以看出最高矩形横轴上的中点为7,由此能求出这100名学生参加实践活动时间的众数的估计值;(0.04+0.12+0.15+a+0.05)×2=1,求出a=0.14,即可求出这100名学生参加实践活动时间的中位数和平均数。
【考点精析】掌握频率分布直方图是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)lnx﹣a(x﹣1).
(1)当a=3时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)设 ![]() ,且a>1,讨论函数g(x)的单调性和极值点.
,且a>1,讨论函数g(x)的单调性和极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=an﹣2anan+1 , an≠0且a1=1.
(1)求数列{an}的通项公式;
(2)令 ![]() ,求数列{bn}的前2n项和T2n .
,求数列{bn}的前2n项和T2n .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有7名学科竞赛优胜者,其中语文学科是A1 , A2 , 数学学科是B1 , B2 , 英语学科是C1 , C2 , 物理学科是D1 , 从竞赛优胜者中选出3名组成一个代表队,要求每个学科至多选出1名.
(1)求B1被选中的概率;
(2)求代表队中有物理优胜者的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为 ![]() .
.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)设P为曲线C1上一点,Q曲线C2上一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:“x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式 ![]() 的解集为N,若x∈N是x∈M的必要不充分条件,求实数a的取值范围.
的解集为N,若x∈N是x∈M的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com