
【题目】已知函数f(x)=(x+1)lnx﹣a(x﹣1).
(1)当a=3时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)设 ![]() ,且a>1,讨论函数g(x)的单调性和极值点.
,且a>1,讨论函数g(x)的单调性和极值点.
【答案】
(1)解:f(x)的定义域为(0,+∞).
当a=3时, ![]() ,
,
f'(1)=﹣1,f(1)=0.
所以曲线y=f(x)在(1,f(1))处的切线方程为x+y﹣1=0
(2)解: ![]() ,x>0,a>1,
,x>0,a>1,
![]() ,
,
令F(x)=x2+2(1﹣a)x+1,其对称轴为x=a﹣1>0,△=4a(a﹣2)
①当△≤0,即1<a≤2,F(x)≥0,g'(x)≥0,
g(x)在(0,+∞)单调递增,无极值.
②当△>0,即a>2,
令g'(x)>0,则 ![]() ,
,
令g'(x)<0,则 ![]()
所以,增区间为 ![]()
减区间为 ![]()
所以,极大值点是 ![]() ,极小值点是
,极小值点是 ![]()
综上:当1<a≤2时,f(x)在(0,+∞)单调递增,无极值.
当a>2时,f(x)在 ![]() 上单调递增,
上单调递增,
在 ![]() 上单调递减;
上单调递减;
极大值点是 ![]() ,极小值点是
,极小值点是 ![]()
【解析】(1)求出函数的导数,计算f(1),f′(1)的值,求出切线方程即可;(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的极值点即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() =1(a>b>0)与双曲线C2:x2﹣
=1(a>b>0)与双曲线C2:x2﹣ ![]() =1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
A.a2= ![]()
B.a2=3
C.b2= ![]()
D.b2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,a∈R.
,a∈R.
(1)求f(x)的解析式;
(2)解关于x的方程f(x)=(a﹣1)4x
(3)设h(x)=2﹣xf(x), ![]() 时,对任意x1 , x2∈[﹣1,1]总有
时,对任意x1 , x2∈[﹣1,1]总有 ![]() 成立,求a的取值范围.
成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 首项为a1且1,an , Sn成等差数列.
(1)求数列{an}的通项公式;
(2)数列{bn}满足bn=(log2a2n+1)×(log2a2n+3),求数列 ![]() 的前n项和Tn .
的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
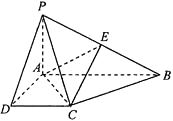
【题目】如图,在四棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证:平面 ![]() 平面
平面 ![]() ;
;
(Ⅱ)试在棱 ![]() 上确定一点
上确定一点 ![]() ,使截面
,使截面 ![]() 把该几何体分成的两部分
把该几何体分成的两部分 ![]() 与
与 ![]() 的体积比为
的体积比为 ![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解全校高中学生五一小长假参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.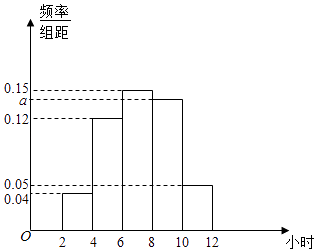
(1)求这100名学生中参加实践活动时间在6~10小时内的人数;
(2)估计这100名学生参加实践活动时间的众数、中位数和平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com