若函数f(x)=x4+ax3+bx2+cx+d.
(1)当a=d=-1,b=c=0时,若函数f(x)的图象与x轴所有交点的横坐标的和与积分别为m,n.
(i)求证:f(x)的图象与x轴恰有两个交点;
(ii)求证:m2=n-n3.
(2)当a=c,d=1时,设函数f(x)有零点,求a2+b2的最小值.
解:(1)(i)当a=d=-1,b=c=0时,f(x)=x
4-x
3-1
∴f'(x)=4x
3-3x
2=x
2(4x-3),
所以

是使f(x)取到最小值的唯一的值,且在区间
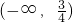
上,函数f(x)单调递减;
在区间
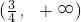
上,函数f(x)单调递增.
因为
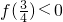
,f(-1)>0,f(2)>0,
所以f(x)的图象与x轴恰有两个交点.
(ii)设x
1,x
2是方程f(x)=0的两个实根,则f(x)有因式(x-x
1)(x-x
2)=x
2-mx+n,
且可令f(x)=(x
2-mx+n)(x
2+px+q).
于是有(x
2-mx+n)(x
2+px+q)=x
4-x
3-1.(*)
分别比较(*)式中常数项和含x
3的项的系数,得nq=-1,p-m=-1,
解得
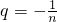
,p=m-1.
所以x
4-x
3-1=
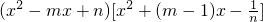
.①
分别比较①式中含x和x
2的项的系数,得
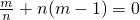
,…②,
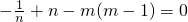
,③
②×m+③×n得-n+n
3+m
2=0,即n-n
3=m
2.
∴m
2=n-n
3.
(2)方程化为:
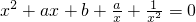
,
令
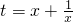
,方程为t
2+at+b-2=0,|t|≥2,即有绝对值不小于2的实根.
设g(t)=t
2+at+b-2=0(|t|≥2),
当
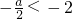
,即a>4时,只需△=a
2-4b+8≥0,此时,a
2+b
2≥16;
当
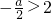
,即a<-4时,只需△=a
2-4b+8≥0,此时,a
2+b
2≥16;
当
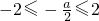
,即-4≤a≤4时,只需(-2)
2-2a+b-2≤0或2
2+2a+b-2≤0,
即-2a+b+2≤0或2a+b+2≤0,此时
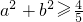
.
∴a
2+b
2的最小值为

.
分析:(1)(i)先求出函数的导函数,然后根据导数符号确定函数的单调性,再根据
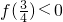
,f(-1)>0,f(2)>0结合根的存在性定理可证得结论;
(ii)设x
1,x
2是方程f(x)=0的两个实根,则f(x)有因式(x-x
1)(x-x
2)=x
2-mx+n,且可令f(x)=(x
2-mx+n)(x
2+px+q),于是有(x
2-mx+n)(x
2+px+q)=x
4-x
3-1,分别比较该式中常数项和含x
3的项的系数,以及含x和x
2的项的系数,消去p与q可证得结论;
(2)方程化为
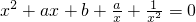
,令
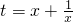
,方程为t
2+at+b-2=0,|t|≥2,即有绝对值不小于2的实根,设g(t)=t
2+at+b-2=0(|t|≥2),讨论对称轴与区间[-2,2]的位置关系,然后建立不等关系,解之即可求出所求.
点评:本题主要考查了函数与方程的综合运用,以及利用导数研究函数的单调性,同时考查了分类讨论的数学思想,属于难题.

 是使f(x)取到最小值的唯一的值,且在区间
是使f(x)取到最小值的唯一的值,且在区间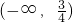 上,函数f(x)单调递减;
上,函数f(x)单调递减;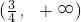 上,函数f(x)单调递增.
上,函数f(x)单调递增.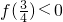 ,f(-1)>0,f(2)>0,
,f(-1)>0,f(2)>0,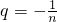 ,p=m-1.
,p=m-1.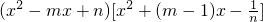 .①
.①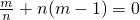 ,…②,
,…②,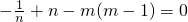 ,③
,③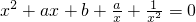 ,
,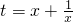 ,方程为t2+at+b-2=0,|t|≥2,即有绝对值不小于2的实根.
,方程为t2+at+b-2=0,|t|≥2,即有绝对值不小于2的实根.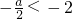 ,即a>4时,只需△=a2-4b+8≥0,此时,a2+b2≥16;
,即a>4时,只需△=a2-4b+8≥0,此时,a2+b2≥16;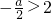 ,即a<-4时,只需△=a2-4b+8≥0,此时,a2+b2≥16;
,即a<-4时,只需△=a2-4b+8≥0,此时,a2+b2≥16;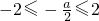 ,即-4≤a≤4时,只需(-2)2-2a+b-2≤0或22+2a+b-2≤0,
,即-4≤a≤4时,只需(-2)2-2a+b-2≤0或22+2a+b-2≤0,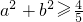 .
. .
.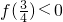 ,f(-1)>0,f(2)>0结合根的存在性定理可证得结论;
,f(-1)>0,f(2)>0结合根的存在性定理可证得结论;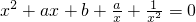 ,令
,令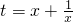 ,方程为t2+at+b-2=0,|t|≥2,即有绝对值不小于2的实根,设g(t)=t2+at+b-2=0(|t|≥2),讨论对称轴与区间[-2,2]的位置关系,然后建立不等关系,解之即可求出所求.
,方程为t2+at+b-2=0,|t|≥2,即有绝对值不小于2的实根,设g(t)=t2+at+b-2=0(|t|≥2),讨论对称轴与区间[-2,2]的位置关系,然后建立不等关系,解之即可求出所求.
