
【题目】已知P是椭圆![]() 上的一点,F1,F2是椭圆的两个焦点。
上的一点,F1,F2是椭圆的两个焦点。
(1)当∠F1PF2=60°时,求△F1PF2的面积;
(2)当∠F1PF2为钝角时,求点P横坐标的取值范围。
【答案】(1) ![]() (2) (-
(2) (-![]() ,
, ![]() )
)
【解析】试题分析:(1)根据椭圆的定义和在![]() 中应用余弦定理,得到
中应用余弦定理,得到![]() 的值,即可求解
的值,即可求解![]() 的面积;
的面积;
(2)由题意![]() 为钝角,得到
为钝角,得到![]() ,进而得到点
,进而得到点![]() 的横坐标的取值范围.
的横坐标的取值范围.
试题解析:
(1)由椭圆的定义,得|PF1|+|PF2|=4且F1(-![]() ,0),F2(
,0),F2(![]() ,0).①
,0).①
在△F1PF2中,由余弦定理,
得|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2| cos60°. ②
由①②得|PF1|·|PF2|=![]() .
.
所以![]() =|PF1||PF2|·sin∠F1PF2=
=|PF1||PF2|·sin∠F1PF2=![]() .
.
(2)设点P(x,y),由已知∠F1PF2为钝角,
得![]() <0,即(x+
<0,即(x+![]() ,y)·(x-
,y)·(x-![]() ,y)<0.
,y)<0.
又y2=1-![]() ,所以
,所以![]() x2<2,解得-
x2<2,解得-![]() <x<
<x<![]() .
.
所以点P横坐标的取值范围是(-![]() ,
, ![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)和g(x)满足f(x)= ![]() e2x﹣2+x2﹣2f(0)x,且g′(x)+2g(x)<0,则下列不等式成立的是( )
e2x﹣2+x2﹣2f(0)x,且g′(x)+2g(x)<0,则下列不等式成立的是( )
A.f(2)g(2015)<g(2017)
B.f(2)g(2015)>g(2017)
C.g(2015)>f(2)g(2017)
D.g(2015)>f(2)g(2017)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C1: ![]() +y2=1,椭圆C2:
+y2=1,椭圆C2: ![]() (a>b>0)的一个焦点坐标为(
(a>b>0)的一个焦点坐标为( ![]() ,0),斜率为1的直线l与椭圆C2相交于A、B两点,线段AB的中点H的坐标为(2,﹣1).
,0),斜率为1的直线l与椭圆C2相交于A、B两点,线段AB的中点H的坐标为(2,﹣1).
(1)求椭圆C2的方程;
(2)设P为椭圆C2上一点,点M、N在椭圆C1上,且 ![]() ,则直线OM与直线ON的斜率之积是否为定值?若是,求出该定值;若不是,请说明理由.
,则直线OM与直线ON的斜率之积是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若对于任意的
,若对于任意的![]() ,,当
,,当![]() 时,都有
时,都有![]() ,则称函数
,则称函数![]() 在
在![]() 上为非减函数.设函数
上为非减函数.设函数![]() 在
在![]() 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() ,则
,则![]() 等于( ).
等于( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥A﹣BCD中,AB、AC、AD两两垂直且长度均为10,定长为 ![]() 的线段MN的一个端点M在棱AB上运动,另一个端点N在△ACD内运动(含边界),线段MN的中点P的轨迹的面积为2π,则m的值等于 .
的线段MN的一个端点M在棱AB上运动,另一个端点N在△ACD内运动(含边界),线段MN的中点P的轨迹的面积为2π,则m的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
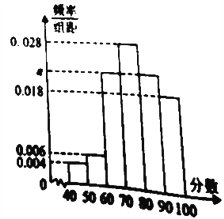
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
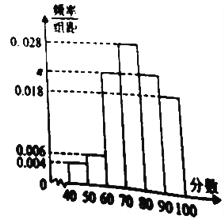
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com