
【题目】函数![]() 的定义域为
的定义域为![]() ,若对于任意的
,若对于任意的![]() ,,当
,,当![]() 时,都有
时,都有![]() ,则称函数
,则称函数![]() 在
在![]() 上为非减函数.设函数
上为非减函数.设函数![]() 在
在![]() 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() ,则
,则![]() 等于( ).
等于( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由赋值法得到f(![]() )=
)=![]() ,f(
,f(![]() )=
)=![]() ,再根据题中的表达式递推得到f(
,再根据题中的表达式递推得到f(![]() )=
)=![]() ,由f(
,由f(![]() )=
)=![]() 及②
及②![]() 得到f(
得到f(![]() )=
)=![]() ,再由题中所给的非减函数得到
,再由题中所给的非减函数得到![]() 可得 f(
可得 f(![]() )≤f(
)≤f(![]() )≤f(
)≤f(![]() ),进而得到结果.
),进而得到结果.
令x=1,由条件求得f(1)=1,f(![]() )=
)=![]() f(1)=
f(1)=![]() ,再由 f(
,再由 f(![]() )+f(
)+f(![]() )=1,由此求得f(
)=1,由此求得f(![]() )=
)=![]() .
.
又∵②![]() ,令x=1,可得 f(
,令x=1,可得 f(![]() )=
)=![]() f(1)=
f(1)=![]() .
.
再由③可得f(![]() )+f(
)+f(![]() )=1,故有f(
)=1,故有f(![]() )=
)=![]() .
.
对于②![]() ,令x=1可得 f(
,令x=1可得 f(![]() )=
)=![]() f(1)=
f(1)=![]() ;
;
由此可得 f(![]() )=
)=![]() f(
f(![]() )=
)=![]() 、f(
、f(![]() )=
)=![]() f(
f(![]() )=
)=![]() 、f(
、f(![]() )=
)=![]() f(
f(![]() )=
)=![]() 、f(
、f(![]() )=
)=![]() f(
f(![]() )=
)=![]() .
.
令x=![]() ,由f(
,由f(![]() )=
)=![]() 及②
及②![]() ,可得 f(
,可得 f(![]() )=
)=![]() ,f(
,f(![]() )=
)=![]() ,f(
,f(![]() )=
)=![]() ,f(
,f(![]() )=
)=![]() .
.
再由![]() 可得 f(
可得 f(![]() )≤f(
)≤f(![]() )≤f(
)≤f(![]() ),即
),即 ![]() ≤f(
≤f(![]() )≤
)≤![]() ,故 f(
,故 f(![]() )=
)=![]() .
.
故答案为:B.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】我国古代秦九韶算法可计算多项式anxn+an﹣1xn﹣1+…+a1x+a0的值,它所反映的程序框图如图所示,当x=1时,当多项式为x4+4x3+6x2+4x+1的值为( ) 
A.5
B.16
C.15
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断当![]() 时函数
时函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)若![]() 定义域为
定义域为![]() ,解不等式
,解不等式![]() .
.
【答案】(1)奇函数(2)增函数(3)![]()
【解析】试题分析:(1)判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。(2)利函数单调性定义证明单调性,按假设,作差,化简,判断,下结论五个步骤。(3)由(1)(2)奇函数![]() 在(-1,1)为单调函数,
在(-1,1)为单调函数,
原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义(-1,1)求解得x范围。
试题解析:(1)函数![]() 为奇函数.证明如下:
为奇函数.证明如下:
![]() 定义域为
定义域为![]()
又![]()
![]() 为奇函数
为奇函数
(2)函数![]() 在(-1,1)为单调函数.证明如下:
在(-1,1)为单调函数.证明如下:
任取![]() ,则
,则


![]()
![]() ,
, ![]()

即![]()
故![]() 在(-1,1)上为增函数
在(-1,1)上为增函数
(3)由(1)、(2)可得
![]() 则
则
 解得:
解得: ![]()
所以,原不等式的解集为![]()
【点睛】
(1)奇偶性:判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。
(2)单调性:利函数单调性定义证明单调性,按假设,作差,化简,定号,下结论五个步骤。
【题型】解答题
【结束】
22
【题目】已知函数![]() .
.
(1)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上是减函数,且对任意的
上是减函数,且对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,且对任意的
,且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,且点
,且点![]() 在
在![]() 上,抛物线
上,抛物线![]() 与椭圆
与椭圆![]() 交于四点
交于四点![]()
(I)求![]() 的方程;
的方程;
(Ⅱ)试探究坐标平面上是否存在定点![]() ,满足
,满足![]() ?(若存在,求出
?(若存在,求出![]() 的坐标;若不存在,需说明理由.)
的坐标;若不存在,需说明理由.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是椭圆![]() 上的一点,F1,F2是椭圆的两个焦点。
上的一点,F1,F2是椭圆的两个焦点。
(1)当∠F1PF2=60°时,求△F1PF2的面积;
(2)当∠F1PF2为钝角时,求点P横坐标的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关系式中正确的是( )
A. sin11°<cos10°<sin168° B. sin168°<sin11°<cos10°
C. sin11°<sin168°<cos10° D. sin168°<cos10°<sin11°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,正方形![]() 所在的平面与正三角形ABC所在的平面互相垂直,
所在的平面与正三角形ABC所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
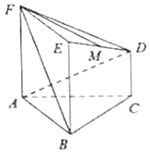
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的标准方程是![]() ,
,
(1)求它的焦点坐标和准线方程.
(2)直线L过已知抛物线的焦点且倾斜角为![]() ,并与抛物线相交于A、B两点,求弦AB的长度.
,并与抛物线相交于A、B两点,求弦AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com