
【题目】已知抛物线的标准方程是![]() ,
,
(1)求它的焦点坐标和准线方程.
(2)直线L过已知抛物线的焦点且倾斜角为![]() ,并与抛物线相交于A、B两点,求弦AB的长度.
,并与抛物线相交于A、B两点,求弦AB的长度.
【答案】(1) 焦点为![]() ,准线方程:
,准线方程: ![]() ;(2) 弦长为16.
;(2) 弦长为16.
【解析】试题分析:(1) 由抛物线的标准方程![]() ,可知焦点在
,可知焦点在![]() 轴的正半轴上,
轴的正半轴上, ![]() ,所以焦点为
,所以焦点为![]() ,准线方程为
,准线方程为![]() ; (2)因为直线L的倾斜角为
; (2)因为直线L的倾斜角为![]() ,所以直线的斜率为
,所以直线的斜率为![]() ,直线L过已知抛物线的焦点,由直线方程的点斜式可得直线的方程为
,直线L过已知抛物线的焦点,由直线方程的点斜式可得直线的方程为![]() ,求直线与抛物线相交弦长,可将直线方程与抛物线方程联立得
,求直线与抛物线相交弦长,可将直线方程与抛物线方程联立得![]() ,设直线与抛物线的两个交点坐标
,设直线与抛物线的两个交点坐标![]() ,由根与系数的关系可得
,由根与系数的关系可得![]() ,代入抛物线的焦点弦长
,代入抛物线的焦点弦长![]() 可求所求弦长。
可求所求弦长。
试题解析: ![]() 抛物线的标准方程是
抛物线的标准方程是![]() ,焦点在x轴上,开口向右,
,焦点在x轴上,开口向右, ![]()
![]() 焦点为
焦点为![]() ,准线方程:
,准线方程: ![]() .
.
![]() 直线L过已知抛物线的焦点且倾斜角为
直线L过已知抛物线的焦点且倾斜角为![]() ,
,
![]() 直线L的方程为
直线L的方程为![]() ,
,
代入抛物线![]() 化简得
化简得![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() .故所求的弦长为16.
.故所求的弦长为16.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若对于任意的
,若对于任意的![]() ,,当
,,当![]() 时,都有
时,都有![]() ,则称函数
,则称函数![]() 在
在![]() 上为非减函数.设函数
上为非减函数.设函数![]() 在
在![]() 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() ,则
,则![]() 等于( ).
等于( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程是 ![]() (φ为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标系方程是
(φ为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标系方程是 ![]() ,正方形ABCD的顶点都在C1上,且A,B,C,D依逆时针次序排列,点A的极坐标为
,正方形ABCD的顶点都在C1上,且A,B,C,D依逆时针次序排列,点A的极坐标为 ![]() .
.
(1)求点A,B,C,D的直角坐标;
(2)设P为C2上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,直线AP,AB,AD两两相互垂直,且AD∥BC,AP=AB=AD=2BC. 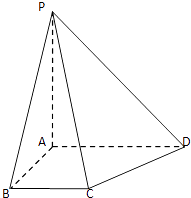
(1)求异面直线PC与BD所成角的余弦值;
(2)求钝二面角B﹣PC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式an=5﹣n,其前n项和为Sn , 将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn , 若存在m∈N* , 使对任意n∈N* , 总有Sn<Tn+λ恒成立,则实数λ的取值范围是( )
A.λ≥2
B.λ>3
C.λ≥3
D.λ>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com