
���� ��1��ֱ�����ü�������ֱ������ת����������⼴�ɣ�
��2����l�IJ������̴���ԲC��ֱ�����귽�̣����ò������̲���t�ļ��������Ƴ�������ɣ�
��� �⣺��1���ɦ�=2$\sqrt{5}$sin�ȵã�x2+y2-2$\sqrt{5}y$=0��x2+��y-$\sqrt{5}$��2=5��
��2����l�IJ������̴���ԲC��ֱ�����귽�̵ã�
$��3-\frac{\sqrt{2}}{2}t��^{2}+��\frac{\sqrt{2}}{2}t��^{2}=5$��t2-3$\sqrt{2}t$+4=0��
���ڡ�=$��3\sqrt{2}��^{2}-4��4=2��0$�ʿ���t1��t2Ϊ���̵���ʵ��
����$\left\{\begin{array}{l}{t}_{1}+{t}_{2}=3\sqrt{2}\\{t}_{1}•{t}_{2}=4\end{array}\right.$��ֱ��l����P��3��$\sqrt{5}$����
������ʽ��t�ļ�������ã�|PA|+|PB|=|t1|+|t2||=t1+t2=3$\sqrt{2}$��
���� ���⿼�鼫������ֱ�����귽�̵Ļ������������̵ļ������壬�������������


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
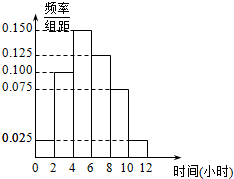 ij��У����ѧ��15 000�ˣ���������10 500�ˣ�Ů��4500�ˣ�Ϊ�����Уѧ��ÿ��ƽ�������˶�ʱ�����������÷ֲ�����ķ������ռ�300λѧ��ÿ��ƽ�������˶�ʱ����������ݣ���λ��Сʱ����
ij��У����ѧ��15 000�ˣ���������10 500�ˣ�Ů��4500�ˣ�Ϊ�����Уѧ��ÿ��ƽ�������˶�ʱ�����������÷ֲ�����ķ������ռ�300λѧ��ÿ��ƽ�������˶�ʱ����������ݣ���λ��Сʱ����| P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
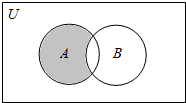
| A�� | {x|x��1} | B�� | {x|0��x��1} | C�� | {x|1��x��2} | D�� | {x|x��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| �����ಡ | δ�����ಡ | �ϼ� | |
| ÿһ�������� | 3 | 17 | a= |
| ������ | 2 | 128 | b= |
| �ϼ� | c= | d= | n= |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| y1 | y2 | �ܼ� | |
| x1 | a | 21 | 73 |
| x2 | 8 | 25 | 33 |
| �ܼ� | b | 46 |
| A�� | 94��96 | B�� | 52��50 | C�� | 52��60 | D�� | 54��52 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com