
正方形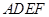 与梯形
与梯形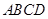 所在平面互相垂直,
所在平面互相垂直,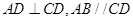 ,
,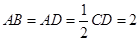 ,点
,点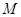 在线段
在线段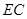 上且不与
上且不与 重合。
重合。
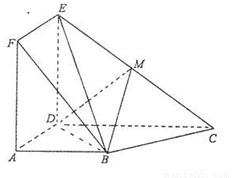
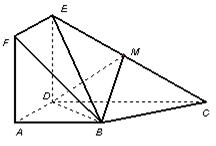
(Ⅰ)当点M是EC中点时,求证:BM//平面ADEF;
(Ⅱ)当平面BDM与平面ABF所成锐二面角的余弦值为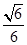 时,求三棱锥
时,求三棱锥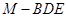 的体积.
的体积.
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:2012-2013学年辽宁省沈阳市四校协作体高三上学期期中联考理科数学试卷 (解析版) 题型:解答题
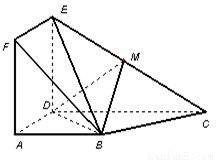
如图,正方形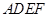 与梯形
与梯形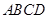 所在的平面互相垂直,
所在的平面互相垂直,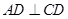 ,
,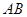 ∥
∥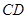 ,
,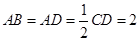 ,点
,点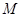 在线段
在线段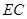 上.
上.
(I)当点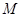 为
为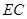 中点时,求证:
中点时,求证: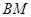 ∥平面
∥平面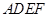 ;
;
(II)当平面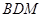 与平面
与平面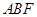 所成锐二面角的余弦值为
所成锐二面角的余弦值为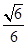 时,求三棱锥
时,求三棱锥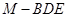 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年海南省高三高考极限压轴卷理科数学试卷(解析版) 题型:填空题
(本小题满分12分)
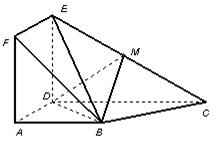
如图,正方形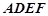 与梯形
与梯形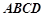 所在的平面互相垂直,
所在的平面互相垂直,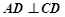 ,
,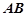 ∥
∥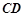 ,
,
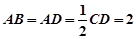 ,点
,点 在线段
在线段 上.
上.
(I)当点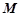 为
为 中点时,求证:
中点时,求证: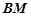 ∥平面
∥平面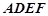 ;
;
(II)当平面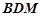 与平面
与平面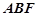 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求三棱锥
时,求三棱锥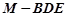 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ∥
∥![]() ,
,
![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
(I)当点![]() 为
为![]() 中点时,求证:
中点时,求证:![]() ∥平面
∥平面![]() ;
;
(II)当平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com