
| A. | $\sqrt{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{3}$ |
分析 由已知利用向量的数量积求出$\overrightarrow{a},\overrightarrow{b}$的夹角,利用向量的运算法则作出图形,结合图形可知O,B,C,A四点共圆.通过正弦定理求出外接圆的直径,求出|$\overrightarrow{c}$|最大值.
解答 解:∵$|{\overrightarrow a}|=|{\overrightarrow b}|=1$,且$\overrightarrow{a}•\overrightarrow{b}$=$-\frac{1}{2}$,∴$\overrightarrow{a},\overrightarrow{b}$的夹角为120°,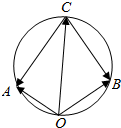
设$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$,
则$\overrightarrow{CA}=\overrightarrow{a}-\overrightarrow{c},\overrightarrow{CB}=\overrightarrow{b}-\overrightarrow{c}$,如图所示,
则∠AOB=120°;∠ACB=60°
∴∠AOB+∠AOC=180°
∴A,O,B,C四点共圆,
∵$\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}$,
∴$|\overrightarrow{AB}{|}^{2}=|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=|\overrightarrow{a}{|}^{2}-2\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}$=3,
∴|$\overrightarrow{AB}$|=$\sqrt{3}$.
由三角形的正弦定理得外接圆的直径2R=$\frac{AB}{sin∠ACB}=2$,
当OC为直径时,|$\overrightarrow{c}$|最大,最大为2.
故选:C.
点评 本题考查向量的数量积公式、向量的运算法则、四点共圆的判断定理、三角形的正弦定理等知识,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
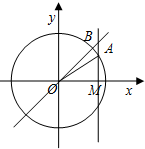 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{37}{21}$ | D. | $\frac{19}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com